Question 1061350: Thomas went to the store and spent half of his money and then $8 more. He went to a second store, spent half of his remaining money and then $8 more. Given that he had $7 left, how many dollars did he start with?
Found 3 solutions by LynnMomo, ikleyn, MathTherapy:
Answer by LynnMomo(10)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let x be amount of money Thomas started with.
First store: $ (x/2 +8)
Second store:$ {[x-(x/2 +8)]/2 +8}
If he had $7 left:
X- first store-second store= $7
X- (x/2+8)- [x-(x/2 +8)]/2 +8= 7
X-x/2-8-[(x-x/2-8)/2+8]=7
X-x/2-8-(x-x/2-8)/2-8=7
X/2-8-(x/2-8)/2-8=7
X/2-(x/2-8)/2-8-8=7
X/2-(x/2-8)/2-16=7
(X-x/2+8)/2=23
X-x/2+8=46
X-x/2=46-8
X-x/2=38
X/2=38
X=76
$76 is the amount of dollars he started with.
I hope my solution help you in Math.^^
Answer by ikleyn(52787)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Thomas went to the store and spent half of his money and then $8 more. He went to a second store, spent half
of his remaining money and then $8 more. Given that he had $7 left, how many dollars did he start with?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
I will solve the problem without using equations, by moving from the end to the beginning.
1. In the second store Thomas spent half of his remaining money and then $8 more; after that he had $7 left.
In other words,
"remaining money" - ("half of his remaining money" + $8) = $7.
It implies that
"remaining money" - "half of his remaining money" = $7 + $8 = $15, or
"half of his remaining money" = $15.
It implies, in turn, that "remaining money" = $30.
So, we derived that "remaining money" amount after shopping in the first store was $30.
2. In the first store Thomas spent half of his money and then $8 more; after that he had $30 left (as we just concluded from the step #1).
In other words,
"Total original money" - ("half of the total original money" + $8) = $7.
It implies that
"The total original money" - "half of the total original money" = $30 + $8 = $38, or
"half of the total original money" = $38.
Now, everybody can conclude that "total original money" = two times $38, or $76.
Answer. Thomas started with $76.
Solved.
The solution by "LynnMomo" is wrong.
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Thomas went to the store and spent half of his money and then $8 more. He went to a second store, spent half of his remaining money and then $8 more. Given that he had $7 left, how many dollars did he start with?
I'll do the problem from the beginning
Let initial amount he had, be A
After spending half of his money, plus $8 at the 1st store, he had:  left left
After spending half of the remainder, plus $8 at the 2nd store, he had:  left left
Since he had $7 left, we get: 
A – 48 = 28 ------ Multiplying by LCD, 4
A, or initial amount he had was 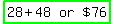
|
|
|