SOLUTION: Log 36 2 + Log 2 6 + Log 36 3 - Log 2 24

Algebra ->  Logarithm Solvers, Trainers and Word Problems -> SOLUTION: Log 36 2 + Log 2 6 + Log 36 3 - Log 2 24       Log On


   

Question 1061208: Log 36 2 + Log 2 6 + Log 36 3 - Log 2 24

Found 2 solutions by Edwin McCravy, math_helper:
Answer by Edwin McCravy(20060) About Me  (Show Source):
You can put this solution on YOUR website!



Break 36 into prime factorization:

   36%22%22=%22%224%2A9%22%22=%22%222%2A2%2A3%2A3%22%22=%22%222%5E2%2A3%5E2 












%284%2B6%2B6-24%29log%28%282%29%29%2B%284%2B6%29log%283%29

-8%2Alog%28%282%29%29%2B10%2Alog%28%283%29%29

Edwin

Answer by math_helper(2461) About Me  (Show Source):
You can put this solution on YOUR website!
I assume the first number after "log" is the base. Thus, I assume the problem is
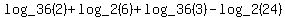
+log_36%282%29+%2B+log_2%286%29+%2B+log_36%283%29+-+log_2%2824%29+
—
Remember, if k = log_b(a) then +b%5Ek+=+a+
In words, the log of a, base b, (here set to k) is the power to which b must be raised to return the original number a.
—
It may seem crazy to use such a mathematical tool like this, but the reason is important. When working with log's (mathematicians would say "working in the log domain"), you can add log's together where you would've needed to otherwise multiply, you can subtract log's where you would have needed to divide, you can multiply exponent*log where you would've had to raise a number to an exponent, etc. A lot of things occurring in nature tend to have exponents in them and often times operating in the log domain on those is faster for a computer program, for example.
—
0.193426 + 2.58496 + 0.30657 - 4.58596 = -1.501004
—
Ans: -1.501004
====
The numbers above correspond to the terms from the original problem. You may wonder where, for example, 0.193426 came from, or how to find it yourself. That number is the exponent to which 36 must be raised in order to give us the number 2: +36%5E0.193426+=+2+ but how did I calculate it? I used the 'Log' button on my calculator. You may now ask, but that uses base=10, so how did you get base=36? Here it is: Log_36(n) = log_10(n)/log_10(36) This can be used for ANY base, and the beauty of it is it shows the power of working in the log domain.