SOLUTION: A scientist has two solutions, which she has labeled Solution A and Solution B. Each contains salt. She knows that Solution A is 65% salt and Solution B is 80% salt. Sh

Algebra ->  Customizable Word Problem Solvers  -> Mixtures -> SOLUTION: A scientist has two solutions, which she has labeled Solution A and Solution B. Each contains salt. She knows that Solution A is 65% salt and Solution B is 80% salt. Sh      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 1060952: A scientist has two solutions, which she has labeled Solution A and Solution B. Each contains salt. She knows that Solution A is
65%
salt and Solution B is
80%
salt. She wants to obtain
30
ounces of a mixture that is
70%
salt. How many ounces of each solution should she use?
Found 2 solutions by josgarithmetic, ikleyn:
Answer by josgarithmetic(39617) About Me  (Show Source):
You can put this solution on YOUR website!
Impossible. About the highest salt concentration in water is about 38%, depending on temperature.

If you only care about the arithmetic and are not interested in what is realistic, then you could use this:

system%28%2865x%2B80y%29%2F30=70%2Cx%2By=30%29

Answer by ikleyn(52787) About Me  (Show Source):
You can put this solution on YOUR website!
.
A scientist has two solutions, which she has labeled Solution A and Solution B. Each contains salt. She knows that Solution A is
65% salt and Solution B is 80% salt. She wants to obtain 30 ounces of a mixture that is 70% salt.
How many ounces of each solution should she use?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ 

I am not a chemist, but know (from the school, from the literature, from "the air") that at normal conditions 
the maximal possible concentration of salt (common table salt NaCl) in water is about 37%.

You can read more about it from the Internet.

But here, I understand, only the Math problem is considered without questioning on feasibility.

OK. The solution is as follows:

Let A be the volume of the 65% solution to be mixed, in ounces. 
Then the volume of the 80% solution to be mixed is (30-A) ounces.

Then you have this "salt concentration" balance equation

0.65*A + (30-A)*0.8 = 0.7*30.

Simplify and solve for A:

0.65A + 24 - 0.8A = 21,

0.65A - 0.8A = 21 - 24,

-0.15A = -3,

A = 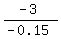%28-3%29%2F%28-0.15%29 = 20.

Answer.  20 ounces of the 65% solution must be mixed with 30-20 = 10 ounces ot the 80% solution.

There is entire bunch of lessons covering various types of mixture problems
    - Mixture problems
    - More Mixture problems
    - Solving typical word problems on mixtures for solutions
    - Word problems on mixtures for antifreeze solutions
    - Word problems on mixtures for alloys
    - Typical word problems on mixtures from the archive
in this site.

Read them and become an expert in solution the mixture word problems.

Also, you have this free of charge online textbook in ALGEBRA-I in this site
    - ALGEBRA-I - YOUR ONLINE TEXTBOOK.

The referred lessons are the part of this textbook in the section "Word problems" under the topic "Mixture problems".