Question 1060919: In triangle ABC, E and F are midpoints of sides line AB and line AC, respectively; and H and I trisect the side BC. If the area of triangle ABC is 120, what is the area of triangle EFJ?
Image is in the link: http://prntscr.com/dhjxtm
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! 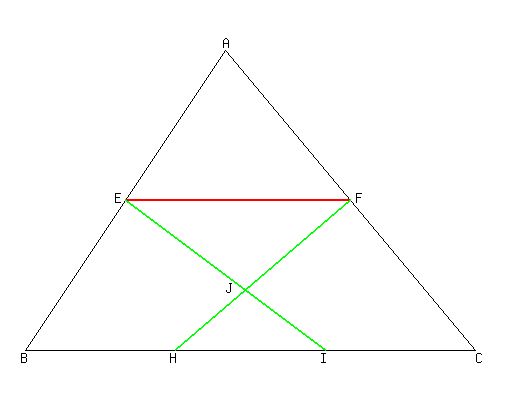
The area of BCA is (1/2)(AB)*h,
with h being the height relative to base BC,
or (in other words, the distance from BC to A).
Because E and F are midpoints of sides AB and AC,
EFA and BCA are similar, EFA being a (1/2) scale version of BCA,
the height of EFA (distance from EF to A) being (1/2)h.
That makes the distance from AB to EF also (1/2)h,
and makes the area of EFA 1/4 of the area of BCA.
(That is (1/4)120=30 for the area of EFA).
Angles EJF and HJI are congruent because they are vertical angles,
formed by the intersection of lines EI and HF.
Angles JIH=EIH=EIB and FEJ=FEI are also congruent because they are alternate interior angles.
formed between parallel lines BC and EF by trasversal EI.
That makes triangles HIJ and EFJ similar triangles.
The length of their bases, EF={1/2)AB, and HI=(1/3)AB are in a 3:2 ratio.
The ratio of the heights relative to those bases is also 3/2.
Their heights add up to (1/2)h, the distance between AB and EF.
That makes the height of HIJ (2/5)(1/2)h=(2/10)h,
and the height of EFJ (3/5)(1/2)h=(3/10)h.
The area of EFJ, with a base (1/2) of the base of BCA,
and a height (3/10) of the height of BCA,
is (1/2)(3/10)=3/20 of the area of BCA.
So Area of EFJ=(3/20)120=3*6= . .
|
|
|