Question 1060283: how many regular polygons are possible whose value of internal angle is a whole number?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! The question obviously refers to the measure of the internal angle in degrees,
because measures of internal angles in radians could never be rational numbers.
An internal angle is supplementary to an external angle,
so the measure in degrees of the internal angle will be an integer if an only if the measure of the external angle is an integer.
The sum of the measures of the external angles is  , ,
so the external angles of a regular polygon with  sides measure sides measure 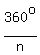 . .
Since  , it has , it has  factors. factors.
Those factor, in pairs are:
1 and 360,
2 and 180,
3 and 120,
4 and 90,
5 and 72,
6 and 60,
8 and 45,
9 and 40,
10 and 36,
12 and 30,
15 and 24,
18 and 20.
However, there are no polygons with 1 or 2 sides,
so there are  types of regular polygons whose external and internal angles have degree measures that are integer numbers. types of regular polygons whose external and internal angles have degree measures that are integer numbers.
With n=3, we have equilateral triangles. Their external angles measure  , and their internal angles measure , and their internal angles measure  . .
With n=4, we have squares. Their external angles measure  , and their internal angles measure , and their internal angles measure  . .
With n=5, we have regular pentagons. Their external angles measure  , and their internal angles measure , and their internal angles measure  . .
With n=6, we have regular hexagons. Their external angles measure  , and their internal angles measure , and their internal angles measure  . .
With n=8, we have regular octagons. Their external angles measure  , and their internal angles measure , and their internal angles measure  . .
Regular polygons with 9, 10, 12, 15, 18, 20, 24, 30, 36, 40, 45, 60, 72, 90, 120, 180, and 360 sides also have internal angles whose measure in degrees is an integer. For a regular polygon with 360 sides, each external angle measures  , and each internal angle measures , and each internal angle measures  . .
|
|
|