Question 1059667: Ana has a piggy bank that contains nickels, dimes, and quarters. When she opens the bank and counts her money, she has $3.35. She counted twice as many nickels as quarters, and two more dimes than quarters. How many dimes does she have?
Found 2 solutions by josgarithmetic, ikleyn:
Answer by josgarithmetic(39618)   (Show Source):
You can put this solution on YOUR website! 
Multiply the money count equation's members by 20, and adjust the ratio equation into n=2q. From that, a substitution for n might be most convenient.
Answer by ikleyn(52790)  (Show Source):
You can put this solution on YOUR website! .
Ana has a piggy bank that contains nickels, dimes, and quarters. When she opens the bank and counts her money, she has $3.35.
She counted twice as many nickels as quarters, and two more dimes than quarters. How many dimes does she have?
~~~~~~~~~~~~~~~~~~~~~~~~~~
Let "x" be the number of quarters in the collection.
Then the number of nickels is 2x and the number of dimes is (x+2), according to the condition.
The nickel contribute 5*(2x) cents to the total.
The dimes contribute 10*(x+2) cents to the total.
the quarters contribute 25x cents to the total.
The total is 5*(2x) + 10*(x+2) + 25x.
Hence, the "value" equation is
5*(2x) + 10*(x+2) + 25x = 335.
Simplify and solve for x:
10x + 10x + 20 + 25x = 335,
45x = 335 - 20,
45x = 315 ---> x = 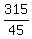 = 7.
Answer. 7 quarters, 2*7 = 14 nickels, 7 + 2 = 9 dimes.
Check. 7*25 + 14*5 + 9*10 = 335 cents. Correct.
The lesson to learn from this solution:
1. First choose the major unknown reasonably.
2. Second, express other unknowns via the major unknown.
3. Then make an equation.
4. Then solve the equation.
It is your algorithm.
--------------------------
There is entire bunch of lessons on coin problems
- Coin problems
- More Coin problems
- Solving coin problems without using equations
- Kevin and Randy Muise have a jar containing coins
- Typical coin problems from the archive
- More complicated coin problems
- Solving coin problems mentally by grouping without using equations
- Santa Claus helps solving coin problem
- OVERVIEW of lessons on coin word problems
in this site.
Read them and become an expert in solution of coin problems.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this online textbook under the topic "Coin problems".
|
|
|
