|
Question 1059625: if a number is 20% more than the other, how much percent is the second number less than the first.
Found 2 solutions by Fombitz, ikleyn:
Answer by Fombitz(32388)   (Show Source): (Show Source):
Answer by ikleyn(52848)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
if a number is 20% more than the other, how much percent is the second number less than the first.
~~~~~~~~~~~~~~~~~~~~~~~~~~~
Let me re-phrase it equivalently in this way:
if a first number is 20% more than the second, how much percent is the second number less than the first.
Let n1 be the first number and n2 be the second number. Then
n1 = 1.2*n2, according to the condition. (We measure numbers in terms of n2 in this case)
(By saying ". . . than n2", we do agree to measure everything in terms of n2)
It means that n2 = 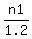 = 0.8(3)*n1. = 0.8(3)*n1.
Hence, n2 is 83.(3)% of n1. (We measure numbers in terms of n1 in this case)
(By saying ". . . than n1", we do agree to measure everything in terms of n1)
In other words, n2 is 16.(6)% less than n1.
Answer. If a first number is 20% more than the second, then the second number is 16.(6)% less than the first.
|
|
|
| |