Question 1059545: Alex, Bob, Charles, and Dan are sitting in a row with the first to fourth places starting from left to right.
How many ways are there if Alex does not sit in the first place, Bob does not sit in the second place,
Charles does not sit in the third place, and Dan does not sit in the fourth place?
Answer by ikleyn(52814)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Let 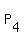 be the set of all sitting arrangements of A, B, C and D in four seats.
As everybody knows, be the set of all sitting arrangements of A, B, C and D in four seats.
As everybody knows, 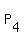 consists of 4*3*2*1 = 24 permutations.
Let consists of 4*3*2*1 = 24 permutations.
Let 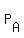 be the subset of all sitting arrangements of A, B, C and D in four seats, where A is sitting in the seat #1.
Let be the subset of all sitting arrangements of A, B, C and D in four seats, where A is sitting in the seat #1.
Let  be the subset of all sitting arrangements of A, B, C and D in four seats, where B is sitting in the seat #2.
Let be the subset of all sitting arrangements of A, B, C and D in four seats, where B is sitting in the seat #2.
Let 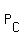 be . . . where C is sitting in the seat #3.
Let be . . . where C is sitting in the seat #3.
Let 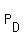 be . . . where D is sitting in the seat #4.
Then be . . . where D is sitting in the seat #4.
Then 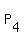 is, oviously, the union of subsets P + is, oviously, the union of subsets P + 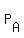 + +  + + 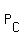 + + 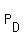 , (1)
where P is our "most desired" subset of those sitting arrangements that are under the problem's question.
It is clear that the cardinality of each subset , (1)
where P is our "most desired" subset of those sitting arrangements that are under the problem's question.
It is clear that the cardinality of each subset 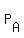 , ,  , , 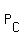 and and 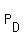 is 6 = 3*2*1.
Therefore, the first desire is to write 24 = |P| + 6 + 6 + 6 + 6, following (1).
But it would not to be correct.
Why? - Because the subsets is 6 = 3*2*1.
Therefore, the first desire is to write 24 = |P| + 6 + 6 + 6 + 6, following (1).
But it would not to be correct.
Why? - Because the subsets 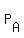 , ,  , , 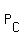 and and 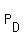 have non-empty intersections that we counted twice.
Did you just get understanding on how to solve the problem and how to proceed?
If not, then follow me.
Let have non-empty intersections that we counted twice.
Did you just get understanding on how to solve the problem and how to proceed?
If not, then follow me.
Let  be the subset of all sitting arrangements of A, B, C and D in four seats, where A and B are sitting in the seats #1 and #2, respectively.
Let be the subset of all sitting arrangements of A, B, C and D in four seats, where A and B are sitting in the seats #1 and #2, respectively.
Let 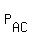 be the subset of all sitting arrangements of A, B, C and D in four seats, where A and C are sitting in the seats #1 and #3, respectively.
Let be the subset of all sitting arrangements of A, B, C and D in four seats, where A and C are sitting in the seats #1 and #3, respectively.
Let 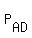 , , 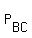 , ,  and and 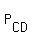 be the other four similar subsets in be the other four similar subsets in 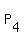 .
Then we can make a correction to formula (1) by writing .
Then we can make a correction to formula (1) by writing
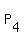 = P + = P + 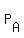 + +  + + 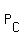 + + 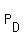 - - 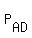 - - 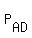 - - 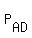 - - 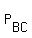 - -  - - 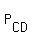 (2)
in the effort to account for double intersections.
But be aware !! This formula is still not exactly correct.
Why? - Because the sets (2)
in the effort to account for double intersections.
But be aware !! This formula is still not exactly correct.
Why? - Because the sets  , , 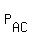 , , 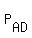 , , 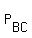 , ,  and and 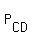 have triple intersections, which we distracted twice in the formula (2).
Did you just get understanding on how to solve the problem and how to proceed?
If not, then follow me again.
Let have triple intersections, which we distracted twice in the formula (2).
Did you just get understanding on how to solve the problem and how to proceed?
If not, then follow me again.
Let 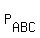 be the subset of all sitting arrangements of A, B, C and D in four seats, where A, B and C are sitting in the seats #1, #2 and #3, respectively.
Let be the subset of all sitting arrangements of A, B, C and D in four seats, where A, B and C are sitting in the seats #1, #2 and #3, respectively.
Let 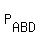 be the subset of all sitting arrangements of A, B, C and D in four seats, where A, B and D are sitting in the seats #1, #2 and #4, respectively.
Let be the subset of all sitting arrangements of A, B, C and D in four seats, where A, B and D are sitting in the seats #1, #2 and #4, respectively.
Let 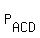 and and 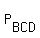 be the other two similar subsets in be the other two similar subsets in 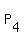 .
At last, let .
At last, let 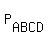 be the subset of all sitting arrangements of A, B, C and D in four seats, where A, B, C and D are sitting in the seats #1, #2, #3 and #4, respectively.
(As you understand, the set be the subset of all sitting arrangements of A, B, C and D in four seats, where A, B, C and D are sitting in the seats #1, #2, #3 and #4, respectively.
(As you understand, the set 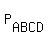 consists of only ONE element, the identical permitation).
Now, finally, we can write the formula which is ABSOLUTELY true! : consists of only ONE element, the identical permitation).
Now, finally, we can write the formula which is ABSOLUTELY true! :
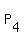 = P + = P + 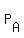 + +  + + 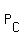 + + 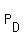 - - 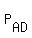 - - 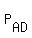 - - 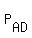 - - 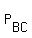 - -  - - 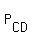 + + 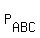 + + 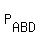 + + 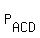 + + 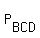 - - 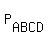 . (3)
I just mentioned above that the cardinality of the 1-letter subsets . (3)
I just mentioned above that the cardinality of the 1-letter subsets 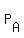 , ,  , , 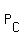 and and 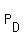 is 6 = 3*2*1.
The cardinality of the 2-letter subsets is 6 = 3*2*1.
The cardinality of the 2-letter subsets  , , 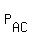 , . . . , , . . . , 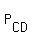 is 2 = 2*1. Obviously.
The cardinality of the 3-letter subsets is 2 = 2*1. Obviously.
The cardinality of the 3-letter subsets 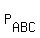 , , 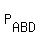 , . . . , , . . . , 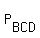 is 1. Obviously.
The cardinality of the 4-letter subsets is 1. Obviously.
The cardinality of the 4-letter subsets 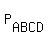 is 1. Obviously.
Therefore, following to the formula (3), we can write its "cardinality" analogue
24 = |P| + (6 + 6 + 6 + 6) - (2 + 2 + 2 + 2 + 2 + 2) + (1 + 1 + 1 + 1) - 1 = |P| + 4*6 - 2*6 + 4 - 1 = |P| + 24 - 12 + 4 - 1 = |P| + 15.
--------------- ----------------------- ---------------
4 times 6 times 4 times
Again, our equation is
24 = |P| + 15.
From here, the cardinality of the set P is |P| = 24 - 15 = 9.
Answer. How many ways are there if Alex does not sit in the first place, Bob does not sit in the second place,
Charles does not sit in the third place, and Dan does not sit in the fourth place? - 9 ways. is 1. Obviously.
Therefore, following to the formula (3), we can write its "cardinality" analogue
24 = |P| + (6 + 6 + 6 + 6) - (2 + 2 + 2 + 2 + 2 + 2) + (1 + 1 + 1 + 1) - 1 = |P| + 4*6 - 2*6 + 4 - 1 = |P| + 24 - 12 + 4 - 1 = |P| + 15.
--------------- ----------------------- ---------------
4 times 6 times 4 times
Again, our equation is
24 = |P| + 15.
From here, the cardinality of the set P is |P| = 24 - 15 = 9.
Answer. How many ways are there if Alex does not sit in the first place, Bob does not sit in the second place,
Charles does not sit in the third place, and Dan does not sit in the fourth place? - 9 ways.
I understand that this solution may seem to be complicated for a novice.
Yes, it would be good to be prepared for such endeavors.
There are two lessons in this site closely related to this theme that I can recommend you:
- Counting elements in sub-sets of a given finite set
- Advanced problems on counting elements in sub-sets of a given finite set
Also, you have these two free of charge online textbooks in ALGEBRA in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
- ALGEBRA-II - YOUR ONLINE TEXTBOOK.
The referred lessons are the parts of these online textbooks under the topic "Miscellaneous word problems".
From my side, it was a pleasure to me to work on this solution.
Thanks for posting this challenging problem.
|
|
|