 Here is the pattern of the binomial theorem for the exponent 8.
Be sure to observe how the pattern goes for any exponent. Also,
"8C3", for instance, means the combinations of 8 things taken
3 at a time.
Here is the pattern of the binomial theorem for the exponent 8.
Be sure to observe how the pattern goes for any exponent. Also,
"8C3", for instance, means the combinations of 8 things taken
3 at a time.
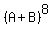

 Substitute for the combinations (binomial coefficients):
Substitute for the combinations (binomial coefficients):
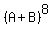

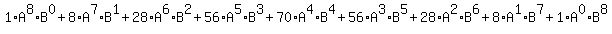 Erase the two 0 powers, the 1 exponents and the 1 coefficients:
Erase the two 0 powers, the 1 exponents and the 1 coefficients:
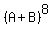

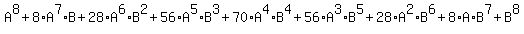 Now substitute (x3) for A:
Now substitute (x3) for A:
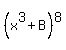

 Simplify the exponents of x:
Simplify the exponents of x:
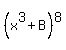

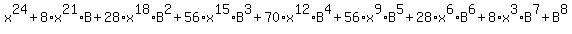
 Since
Since 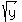

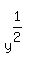 ,
Substitute
,
Substitute 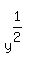 for B:
for B:
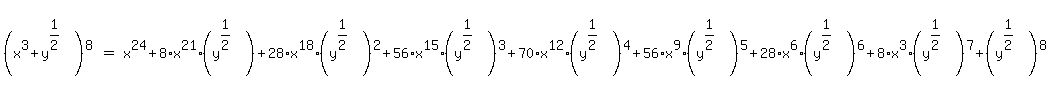 Simplify the exponents of y:
Simplify the exponents of y:
 You can leave it like that, or if you want to, you can
change it back to radicals, by first writing the improper
fraction exponents as mixed fractions:
You can leave it like that, or if you want to, you can
change it back to radicals, by first writing the improper
fraction exponents as mixed fractions:
 Next, write the mixed fractions as the whole part + the fraction part:
Next, write the mixed fractions as the whole part + the fraction part:
 Next write the exponentials (with base y which have exponents
which are sums), as the product of two exponentials of y:
Next write the exponentials (with base y which have exponents
which are sums), as the product of two exponentials of y:
 Finally substitute
Finally substitute 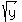 for
for 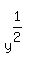
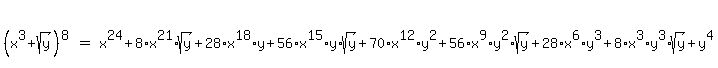 Edwin
Edwin