SOLUTION:   At first a runner jogs at 5 mph and then jogs at 8 mph traveling 7 miles in 1.1 hours. How long does the runner jog at each speed. (Hint: Let t represent the amount of time the

Algebra ->  Customizable Word Problem Solvers  -> Travel -> SOLUTION:   At first a runner jogs at 5 mph and then jogs at 8 mph traveling 7 miles in 1.1 hours. How long does the runner jog at each speed. (Hint: Let t represent the amount of time the       Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 1058945:  
At first a runner jogs at 5 mph and then jogs at 8 mph traveling 7 miles in 1.1 hours. How long does the runner jog at each speed. (Hint: Let t represent the amount of time the runner jogs at 5 mph. Then 1.1 - t represents the amount of time the runner jogs at 8 mph.) Set up an equation for distance at 5 mph + distance at 8 mph = 7miles.
Found 2 solutions by josgarithmetic, ikleyn:
Answer by josgarithmetic(39630) About Me  (Show Source):
You can put this solution on YOUR website!
Make a data table and then use RT=D basic principle to form the necessary equations. 
           SPEED       TIME        DISTANCE

SLOW         5         t

FAST         8

Total                  1.1           7


You need to fill in the missing cells of the data table.
           SPEED       TIME        DISTANCE

SLOW         5         t       5t

FAST         8          x            8x

Total                  1.1           7

The additional variable, x for the FAST time is the only way I can see to do this. You have two sums in the variables, t and x. They are LINEAR equations forming a system.

system%28t%2Bx=1.1%2C5t%2B8x=7%29, and you should be able to solve this system.

Answer by ikleyn(52898) About Me  (Show Source):
You can put this solution on YOUR website!
.
At first a runner jogs at 5 mph and then jogs at 8 mph traveling 7 miles in 1.1 hours. How long does the runner jog at each speed.
(Hint: Let t represent the amount of time the runner jogs at 5 mph. Then 1.1 - t represents the amount of time the runner jogs at 8 mph.)
Set up an equation for distance at 5 mph + distance at 8 mph = 7miles.
~~~~~~~~~~~~~~~~~~~~~

They just explained you how to start your solution:
So, I will start as they recommend: 

"Let t represent the amount of time the runner jogs at 5 mph."
"Then 1.1 - t represents the amount of time the runner jogs at 8 mph."

During time "t" hours the runner jogs the distance of 5*t miles.
During time 1.1-t hours the runner jogs the distance 8*(1.1-t) miles.

In all, the runner will jog 5t + 8*(1.1-t) miles.
Since it is 7 miles, you have this equation

5t + 8*(1.1-t) = 7.

Simplify and solve for "t":

5t + 8.8 - 8t = 7,

-5t = 7 - 8.8,

-3t = -1.8,

t = 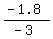%28-1.8%29%2F%28-3%29 = 0.6.

Hence, the runner jogs 0.6 hour = 36 minutes at 5 mph.

The rest of time, 1.1 hour minus 0.6 hour = 0.5 hour = 30 minutes, the runner jogs t 8 mph.

Solved.

And forget on using tables (as "josgarithmetic" recommend) if you want to learn on how to solve such problems.