SOLUTION: Use the factor theorem to prove that x^2 - x - 2 is a factor of x^3 - 6x^2 +3x + 10

Algebra ->  Polynomials-and-rational-expressions -> SOLUTION: Use the factor theorem to prove that x^2 - x - 2 is a factor of x^3 - 6x^2 +3x + 10      Log On


   

Question 1058801: Use the factor theorem to prove that x^2 - x - 2 is a factor of x^3 - 6x^2 +3x + 10
Answer by josgarithmetic(39616) About Me  (Show Source):
You can put this solution on YOUR website!
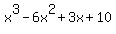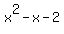What happens if you divide x%5E3-6x%5E2%2B3x%2B10 by x%5E2-x-2? 
x^2-x-2    |     x      -5
           -------------------------------------------
                x^3    -6x^2    +3x    +10
                x^3    -x^2     -2x
                ____________________
                0      -5x^2    5x     10
                       -5x^2   5x      10
                       -------------------
                       0         0     0
Remainder is 0. The divisor IS a factor of the dividend.

As an alternative, what happens if you substitute the given divisor INTO the cubic polynomial dividend and simplify? That work will be much longer; the division shown above is easier.