Question 1058797: In a triathlon, Jenny swim for one hour, bike for 1.75 hours, and ran for one hour. Her average biking speed was two times her average running speed, and her average running speed with eight times her average swimming speed. The total distance of the triathlon was 55.5 km. Calculate Jenny's average swiming speed in kilometers per hour.
Found 3 solutions by josgarithmetic, MathTherapy, ikleyn:
Answer by josgarithmetic(39625)   (Show Source): (Show Source):
You can put this solution on YOUR website! Some values you know (given or calculated) and some things you do not know.
RATE TIME DISTANCE
BIKE 2*8r 1.75
RUN 8r
SWIM r 1
Total 55
Give a variable to unknown running speed and fill in everything.
RATE TIME DISTANCE
BIKE 16r 1.75 28r
RUN 8r t 8rt
SWIM r 1 r
Total 55
Notice some trouble? WHY? I missed seeing the "ran for one hour". the variable t is KNOWN! This will be corrected here:
RATE TIME DISTANCE
BIKE 16r 1.75 28r
RUN 8r 1 8r
SWIM r 1 r
Total 55
Everything is filled and looks good. There is a sum of distances in just the one single variable, r.

Solve for r, and this is the swimming speed.
Answer by MathTherapy(10555)   (Show Source): (Show Source):
You can put this solution on YOUR website! In a triathlon, Jenny swim for one hour, bike for 1.75 hours, and ran for one hour. Her average biking speed was two times her average running speed, and her average running speed with eight times her average swimming speed. The total distance of the triathlon was 55.5 km. Calculate Jenny's average swiming speed in kilometers per hour.
Let swimming speed be S
Then running speed = 8S
Biking speed = 2(8S), or 16S
We then get the following DISTANCE equation: S + 8S + 1.75(16S) = 55.5
Solve for S, the swimming speed and you should get: 
Very, very simple....nothing COMPLEX, regardless of how complex some people may make it!
Answer by ikleyn(52847)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
In a triathlon, Jenny swim for one hour, bike for 1.75 hours, and ran for one hour. Her average biking speed was two times
her average running speed, and her average running speed  was eight times her average swimming speed. was eight times her average swimming speed.
The total distance of the triathlon was 55.5 km. Calculate Jenny's average swiming speed in kilometers per hour.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Let "r" be Jenny's swimming speed, in  .
Then her running speed was 8r,
and her biking speed was 2*(8r) = 16r.
Swimming for 1 hour, Jenny covered the distance of 1*r = r kilometers.
Biking for 1.75 hour, Jenny covered the distance of 1.75*16r = 28r kilometers.
Running for 1 hour, Jenny covered the distance of 1*2r = 8r kilometers.
The total distance Jenny covered was r + 28r + 8r = 37r.
It gives you an equation
37r = 55.5 kilometers.
Then r = .
Then her running speed was 8r,
and her biking speed was 2*(8r) = 16r.
Swimming for 1 hour, Jenny covered the distance of 1*r = r kilometers.
Biking for 1.75 hour, Jenny covered the distance of 1.75*16r = 28r kilometers.
Running for 1 hour, Jenny covered the distance of 1*2r = 8r kilometers.
The total distance Jenny covered was r + 28r + 8r = 37r.
It gives you an equation
37r = 55.5 kilometers.
Then r = 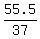 = 1.5 km/h.
It was Jemmy's swimming speed.
Answer. Jemmy's swimming speed was 1.5 km/h. = 1.5 km/h.
It was Jemmy's swimming speed.
Answer. Jemmy's swimming speed was 1.5 km/h.
Lessons to learn from this solution:
1. Think twice or even trice on how to choose the major/leading unknown.
2. Express other data via this unknown.
3. Think how to construct (to make) an equation.
4. If you can do all this steps without making tables, do it without making tables.
It is a preferable way.
5. Remember, that when solving word problems, your major goal is to make an equation.
You will become an expert in solving word problems when (and only when) you will learn on how to write the governing equation
instantly after you read and understand the condition.
|
|
|