Question 1058525: The question I am given is "Find all values of x in the interval [0,2pi], that satisfy sin2x=cosx" I am having some difficulty with understanding why x=2pi/6 and x=4pi/6 are not included in the solution since these angles are reference angles of sin(pi/6) = 1/2, and therefore, should equal to 1/2. But I just computed these angles on my calculator, and they do not equal 1/2...why is that? Thank you in advance!
Answer by ikleyn(52788)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The question I am given is "Find all values of x in the interval [0,2pi], that satisfy sin2x=cosx" I am having some difficulty
with understanding why x=2pi/6 and x=4pi/6 are not included in the solution since these angles are reference angles of sin(pi/6) = 1/2,
and therefore, should equal to 1/2. But I just computed these angles on my calculator, and they do not equal 1/2...why is that?
Thank you in advance!
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Let us consider the angle x = 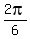 , the first of the two angles you are asking for.
Notice that x = , the first of the two angles you are asking for.
Notice that x = 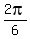 = =  .
Now, .
Now, 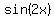 = =  = =  .
From the other side, .
From the other side,  = =  = =  .
So, you see that sin(2x) =/= cos(x) in this case.
Therefore, .
So, you see that sin(2x) =/= cos(x) in this case.
Therefore, 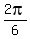 is not included to the list of solutions.
Because it IS NOT a solution. is not included to the list of solutions.
Because it IS NOT a solution.
For many other similar solved problems see the lessons
- Solving simple problems on trigonometric equations
- Solving typical problems on trigonometric equations
- Solving more complicated problems on trigonometric equations
- Solving advanced problems on trigonometric equations
in this site.
|
|
|