Question 1058289: Hikers Mario and Evan start out at the same point. Mario walks due North for x miles. In the same amount of time, Evan, going due east, walks one mile further than Mario walked. When they stop, the distance between the hikers is 2 miles more than the distance walked by Mario. How far did each hiker walk?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website!  = distance walked by Mario, in miles = distance walked by Mario, in miles
 = distance walked by Evan = distance walked by Evan
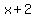 = distance between Mario and Evan at the end of their walks. = distance between Mario and Evan at the end of their walks.
The 3 distances above are the lengths of the sides of a triangle.
Since Mario and Evan walked in directions perpendicular to each other,
their walks are the legs of a right trisngle,
and the final distance between them is the hypotenuse of that triangle.
According to the Pythagorean theorem,





 is the only positive solution, is the only positive solution,
so Mario walked  , ,
and  is the number of miles walked by Evan. is the number of miles walked by Evan.
NOTE:
The triangle is a 3-4-5 triangle,
the most popular right triangle with whole number side lengths,
and the only one with where the long leg and hypotenuse
are longer than the short leg by 1 and 2 units respectively
(as proven above).
Knowing that, no calvulation is needed,
which would be helpful if this was a multiple choice question.
|
|
|