SOLUTION: Dinu & Hemu can plough a field in 15 days . If Dinu alone can plough 1/8 of the field in 5 days , how many days will Hemu take to do the same work alone?

Algebra ->  Rate-of-work-word-problems -> SOLUTION: Dinu & Hemu can plough a field in 15 days . If Dinu alone can plough 1/8 of the field in 5 days , how many days will Hemu take to do the same work alone?      Log On


   

Question 1058142: Dinu & Hemu can plough a field in 15 days . If Dinu alone can plough 1/8 of the field in 5 days , how many days will Hemu take to do the same work alone?
Found 2 solutions by josgarithmetic, ikleyn:
Answer by josgarithmetic(39618) About Me  (Show Source):
You can put this solution on YOUR website!
Dinu and Hemu do 1 job in 15 days.
Dinu does 1%2F8 the job in 5 days.
Just Hemu needs h days for 1 job.
Dinu does 1 job in d days.

system%281%2Fd%2B1%2Fh=1%2F15%2C%281%2Fd%29%2A5=1%2F8%29

Simplifying each equation,
-
dh%281%2Fd%2B1%2Fh%29=dh%281%2F15%29
h%2Bd=dh%2F15
15h%2B15d=dh
-
5%2Fd=1%2F8
d=40
Already the time needed for Dinu for 1 job.

15h%2B15%2A40=40%2Ah
15%2A40=%2840-15%29h
25h=15%2A5%2A8
h=%283%2A5%2A5%2A8%29%2F%285%2A5%29
highlight%28h=24%29

Answer by ikleyn(52793) About Me  (Show Source):
You can put this solution on YOUR website!
.
Dinu & Hemu can plough a field in 15 days . If Dinu alone can plough 1/8 of the field in 5 days ,
how many days will Hemu take to do the same work alone?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ 

If Dinu alone can make 1/8 of the job in 5 days then Dinu can do the entire job in 8*5 = 40 days.

Now, Dinu and Hemu can make 1%2F15 of the job per day, working together, as we know from the condition.

From the other side, Dinu can make 1%2F40 of the job per day, working alone.

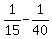Hence, Hemu makes 1%2F15+-+1%2F40 of the work per day, working alone.

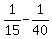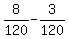1%2F15+-+1%2F40 = 8%2F120+-+3%2F120 = 5%2F120 = 1%2F24.

If Hemu makes 1%2F24 of the work per day, he can complete the entire job in 24 days, working alone.

Answer.  Hemu can complete the entire job in 24 days, working alone.


The lesson to learn from this solution:

     There is no need to solve equations.
     You can solve it using simple logic.
     You also are supposed to operate freely with fractions. That's all.

     Simple logic and fractions.


-------------------------------------------
There is a bunch of lessons on similar joint-work problems with detailed explanations
    - Using Fractions to solve word problems on joint work,
    - Solving more complicated word problems on joint work,
    - Selected joint-work word problems from the archive
in this site.

Read them and get be trained in solving joint-work problems.

Also, you have this free of charge online textbook in ALGEBRA-I in this site
    - ALGEBRA-I - YOUR ONLINE TEXTBOOK.

The referred lessons are the part of this textbook under the topic "Rate of work and joint work problems" of the section "Word problems".