.
Find the general solution √3cosx+sinx=1
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
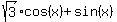 =
=  .
Multiply both sides by
.
Multiply both sides by  . You will get
. You will get
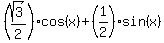 =
=  . (1)
Notice that
. (1)
Notice that  =
=  ,
,  =
=  .
Substitute it into the left side of (1). You will get
.
Substitute it into the left side of (1). You will get
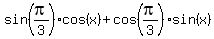 =
=  . (2)
Apply the formula sin(a)*cos(b) + cos(a)*sin(b) = sin(a+b) to the left side of (2). You ill get
. (2)
Apply the formula sin(a)*cos(b) + cos(a)*sin(b) = sin(a+b) to the left side of (2). You ill get
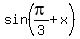 =
=  . (3)
It implies
. (3)
It implies
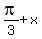 =
=  , k = 0, +/-1, +/-2, . . . or
, k = 0, +/-1, +/-2, . . . or
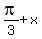 =
=  , k = 0, +/-1, +/-2, . . .
Thus there are two sets of solutions:
1. x =
, k = 0, +/-1, +/-2, . . .
Thus there are two sets of solutions:
1. x = 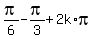 =
= 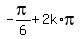 , which is equivalent to x =
, which is equivalent to x = 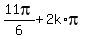 ,
and the other family
2. x =
,
and the other family
2. x = 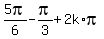 =
= 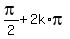 Answer. There are two sets of solutions: 1) x =
Answer. There are two sets of solutions: 1) x = 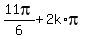 and 2) x =
and 2) x = 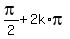 , k = 0, +/-1, +/-2, . . .
, k = 0, +/-1, +/-2, . . .
The plot below confirms these solutions.

Plots y = 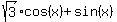 and y = 1
and y = 1