|
Question 1058038: Jack and Jill together can do a piece of work in 3 days.
They can finish the work if Jack works for 2 days and Jill
works for 4 days. Find the time required for each to do the
work.
Found 2 solutions by Edwin McCravy, ikleyn:
Answer by Edwin McCravy(20060)   (Show Source): (Show Source):
You can put this solution on YOUR website! Jack and Jill together can do a piece of work in 3 days.
They can finish the work if Jack works for 2 days and Jill
works for 4 days. Find the time required for each to do the
work.
Let the time for Jack to do the job = x days
So Jack's rate in jobs per day is
1 job per x days or
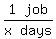 ,
so his rate in jobs/day is ,
so his rate in jobs/day is
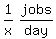 ---
Let the time for Jill to do the job = y days
So Jill's rate in jobs per day is
1 job per y days or
---
Let the time for Jill to do the job = y days
So Jill's rate in jobs per day is
1 job per y days or
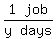 ,
so her rate in jobs/day is ,
so her rate in jobs/day is
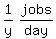 We look at the second sentence first:
We look at the second sentence first:
They can finish the work if Jack works for 2 days
and Jill works for 4 days.
In 2 days, using
production = rate × time, Jack's production = 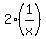 or or 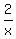 .
In 4 days, using
production = rate × time, Jill's production = .
In 4 days, using
production = rate × time, Jill's production = 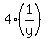 or or 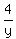 .
Since they finish 1 job, .
Since they finish 1 job,
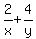   Now we look at the first sentence:
Now we look at the first sentence:
Jack and Jill together can do a piece of work in 3 days.
Their combined rate is the sum of their rates, so
Their combined rate = 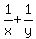 So in 3 days, using
production = rate × time, the production =
So in 3 days, using
production = rate × time, the production = 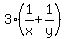 or or 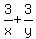 .
Since they finish 1 job, .
Since they finish 1 job,
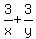   So the system of equations is
So the system of equations is
 Adding them term by term gives:
Adding them term by term gives:
 Multiply both sides by y
Multiply both sides by y
 So Jack can do the job in 6 days.
Substituting y=6 in
So Jack can do the job in 6 days.
Substituting y=6 in


 Multiply through by 3x
Multiply through by 3x

 So Jill can also do the job in 6 days.
They can each do the job working alone in 6 days.
Edwin
So Jill can also do the job in 6 days.
They can each do the job working alone in 6 days.
Edwin
Answer by ikleyn(52832)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Jack and Jill together can do a piece of work in 3 days.
They can finish the work if Jack works for 2 days and Jill
works for 4 days. Find the time required for each to do the
work.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Since "Jack and Jill together can do a piece of work in 3 days", they do  of the job working together.
The next phrase of the condition says:
"They can finish the work if Jack works for 2 days and Jill works for 4 days."
You can re-phrase it in this equivalent way:
They can finish the work if Jack and Jill work together for 2 days and then Jill works for additional 2 days.
OK, very good.
But then, working 2 days together, Jack and Jill will do of the job working together.
The next phrase of the condition says:
"They can finish the work if Jack works for 2 days and Jill works for 4 days."
You can re-phrase it in this equivalent way:
They can finish the work if Jack and Jill work together for 2 days and then Jill works for additional 2 days.
OK, very good.
But then, working 2 days together, Jack and Jill will do  of the job.
It means that Jill can complete the remaining of the job.
It means that Jill can complete the remaining  of the job in two days.
Hence, Jill can complete the entire job in 6 days.
Half of the problem is just solved. Now we can easily complete the rest, too.
Since Jill does the entire job in 6 days, in three days she makes of the job in two days.
Hence, Jill can complete the entire job in 6 days.
Half of the problem is just solved. Now we can easily complete the rest, too.
Since Jill does the entire job in 6 days, in three days she makes  of the job.
It means that in 3 day Jack makes the remaining of the job.
It means that in 3 day Jack makes the remaining  of the job.
In turn, it means that Jack can do the entire work in 6 days. of the job.
In turn, it means that Jack can do the entire work in 6 days.
Solved.
The lesson to learn from this solution:
There is no need to solve equations.
You can solve it using simple logic.
You also are supposed to operate freely with fractions. That's all.
Simple logic and fractions.
----------------------------------------
There is a bunch of lessons on similar joint-work problems with detailed explanations
- Using Fractions to solve word problems on joint work,
- Solving more complicated word problems on joint work,
- Selected joint-work word problems from the archive
in this site.
Read them and get be trained in solving joint-work problems.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this textbook under the topic "Rate of work and joint work problems" of the section "Word problems".
|
|
|
| |