.
A block of mass m1 = 3.00 kg slides along a frictionless table with a speed of 13.0 m/s. Directly in front of it,
and moving in the same direction, is a block of mass m2 = 4.00 kg moving at 1.00 m/s. A massless spring with a spring constant
k = 1620 N/m is attached to the backside of m2. When the blocks collide, what is the maximum compression (in meters) of the spring?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
When solving the Physics problems like this one, the key is clearly to understand what happens with the system and what Physics law/laws to apply.
What is the time moment when the maximum compression of the spring occurs?
How do the two bodies move at this time moment?
It is very simple.
At this time moment the two bodies move with equal speeds.
It is the key.
Before this time moment and after it the bodies move with different velocities.
But in THIS particular time moment the two bodies have equal velocities. Their relative speed is ZERO at this time moment.
So, in this time moment the collision is similar "perfectly INELASTIC collision".
Before this time moment and after it, the behavior of the bodies is different, but
exactly at this moment it is like "perfectly INELASTIC collision":
In this particular time moment the two mass moves "together" as one whole mass.
Very good. Then you can apply the "momentum conservation law".
It says that the momentum before the collision is equal to momentum after collision.
The momentum before the collision was 3*13 + 4*1 (kg*m/s).
The momentum at the "perfectly INELASTIC collision" is (3+4)*V,
where (3+4) kg is the sum of masses and "V" is their unknown common speed.
So, the "momentum conservation law" is this equation
3*13 + 4*1 = (3+4)*V,
which allows you to find the common speed of the two bodies
V =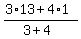 
= 
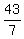m/s
at the particular moment of maximal spring compression.
Now we are on the finish line.
The initial kinetic energy of the two bodies (before they contacted via the spring) was
= 
+ 
.
The kinetic energy of the "clued" mass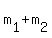 
at the "perfectly INELASTIC collision" is
= 
.
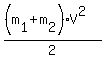The difference - is the potential energy of the compressed spring 
( !! Yes, the "Energy conservation law" !!! ).
where k = 1620 N/m is the spring constant and "x" is the maximum compression of the spring.
So, your equation to find "x" is
+ - = .
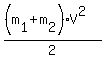Substitute the given data and (just found value of) V and find "x".
Solved !
------------------------------
Would you mind to answer couple of my questions.
Are you at high school or college?
Which textbook do you use?
