Question 1057242: A collection of coins consisting of dimes and quarters has a value of $2.55. If the number of dimes is 3 more than twice the number of quarters, how many of each type of coin are there?
Found 2 solutions by ikleyn, MathTherapy:
Answer by ikleyn(52790)   (Show Source):
You can put this solution on YOUR website! .
A collection of coins consisting of dimes and quarters has a value of $2.55. If the number of dimes is 3 more
than twice the number of quarters, how many of each type of coin are there?
~~~~~~~~~~~~~~~~~~~~~~~~~~
From the condition, you have these two equations
10d + 25q = 255, (1)
d = 2q + 3. (2)
substitute expression (2) to the equation (1), replacing d. You will get
10(2q +3) + 25q = 255, or
20q + 30 + 25q = 255, or
45q = 255 - 30,
45q = 225.
q = 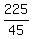 = 5
5 quarters and 2*5 + 3 = 13 dimes.
Sorry, it was MY mistake.
Answer by MathTherapy(10552)  (Show Source):
You can put this solution on YOUR website!
A collection of coins consisting of dimes and quarters has a value of $2.55. If the number of dimes is 3 more than twice the number of quarters, how many of each type of coin are there?
|
|
|
