Question 1057131: I just need someone to explain this and why 2 is the answer:
3^(log base 9 (4))= 2
I'm not sure how to write out log base correctly, but it's log(4) with the base of 9.
Found 4 solutions by solve_for_x, josgarithmetic, ikleyn, MathTherapy:
Answer by solve_for_x(190)   (Show Source): (Show Source):
Answer by josgarithmetic(39618)   (Show Source): (Show Source):
Answer by ikleyn(52790)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
I just need someone to explain this and why 2 is the answer:
3^(log base 9 (4))= 2
I'm not sure how to write out log base correctly, but it's log(4) with the base of 9.
~~~~~~~~~~~~~~~~~~~~~~~
The problem is solved in two steps:
1. 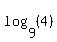 = = 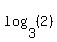 Indeed, if
Indeed, if 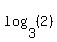 = x, it means (by the definition of logarithm) that = x, it means (by the definition of logarithm) that 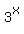 = 2.
Then = 2.
Then 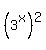 = = 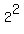 = 4, which implies = 4, which implies 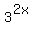 = 4, which is the same as = 4, which is the same as 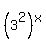 = 4, or = 4, or 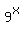 = 4.
The last equality means that = 4.
The last equality means that 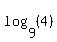 = x. Hence, = x. Hence, 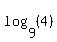 = = 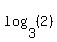 , QED.
2. , QED.
2. 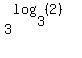 = 2. (<---- = 2. (<---- 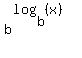 = x for any x > 0 and for any b > 0, b=/= 1.
This is the basic property of the logarithm, equivalent to the definition of the logarithm) = x for any x > 0 and for any b > 0, b=/= 1.
This is the basic property of the logarithm, equivalent to the definition of the logarithm)
On logarithms, see the lessons
- WHAT IS the logarithm
- Properties of the logarithm
in this site.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this online textbook under the topic "Logarithms".
Answer by MathTherapy(10552)   (Show Source): (Show Source):
|
|
|