Question 1057012: Find the probability of randomly choosing a prime number when picking a number between 1 and 100.
Found 4 solutions by Alan3354, kittygoesmeow, ikleyn, MathTherapy:
Answer by Alan3354(69443)   (Show Source):
You can put this solution on YOUR website! A no. Chosen between 1 to 100 find the probability of getting a prime no.
-------
Count the # of primes, call it n.
Probability = n/100
=======================
There are 25 primes, the 23 listed by another tutor and 43 & 67.
------------
25/100 = 1/4
--------------------
It's true that 1 is not a prime number, but it might still be chosen.
Answer by kittygoesmeow(1)  (Show Source):
You can put this solution on YOUR website! The primes from 1 to 100 are: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 47, 53, 59, 61, 71, 73, 79, 83, 89, and 97; so there are 23 numbers between 1 and 100 and the probability of getting one of them is 23/100.
Answer by ikleyn(52824)  (Show Source):
You can put this solution on YOUR website! .
Find the probability of randomly choosing a prime number when picking a number between 1 and 100.
~~~~~~~~~~~~~~~~~~~~~~~~~~
In the solution of the previous tutor the prime number 67 was omitted.
So the answer is  =  .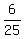
Answer by MathTherapy(10555)  (Show Source):
You can put this solution on YOUR website!
Find the probability of randomly choosing a prime number when picking a number between 1 and 100.
Numbers between 1 and 100 EXCLUDE 1 and 100. Furthermore, as we well know, 1 is not prime. Primes are > 1. Therefore, there are 98 numbers that you can choose from,
and since there are 25 PRIMES BETWEEN 1 and 100, we get: 
|
|
|
