In a nutshell, it is always wrong to assume something that is not
given.
When we work with both sides of an equation, we are assuming that
both sides are already equal. But in the case of proving identities,
we must begin WITHOUT assuming that both sides are equalfor
It would be much better if a question mark were placed over the equal
sign, i.e., that the symbol
≟
were used instead of just an equal sign or identity symbol. That is,
it would be better if textbooks and teachers would write this:
≟ 
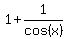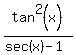instead of this
=
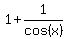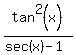The very fact that there is an equal or identity sign already
there does cause students to get the false illusion that the two
sides are already given equal, when that is not given, but rather
is, instead, what is to be proved.
Now your second question is a bit puzzling because it would always
"make a difference" to do something mathematically incorrect instead
of doing what is mathematically legal. However if what is given is
truly an identity which can proved, then even if we break the
rules and go ahead and work with both sides, we will always get a
result which is an equivalent equation. So quite obviously we
cannot start out with a true equation, work with both sides, and
end up with a false equation! This is why students who break the
rules and work with both sides, end up with the same expression on
both sides, and falsely think they have proved the identity, when
they haven't at all.
Edwin
