Question 1056129: At fundraising event for a local kindergarten school, a total of $400 have been collected in three different types of denominations: $5 s, $10 bills and $20 bills. There were four more $10 bills than $20 bills, and there were twice as many $5 bills as $20 bills. Find the number of $5 bills , the number of $10 bills and the number of $20 bills
Answer by ikleyn(52903)   (Show Source):
You can put this solution on YOUR website! .
At fundraising event for a local kindergarten school, a total of $400 have been collected in three different types of denominations:
$5 s, $10 bills and $20 bills. There were four more $10 bills than $20 bills, and there were twice as many $5 bills as $20 bills.
Find the number of $5 bills , the number of $10 bills and the number of $20 bills
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
x for $20 bills.
Then the number of the $10 bills is (x+4),
and the number of the $5 bills is 2x.
$5 dollar bills contribute 5*(2x) to the total.
$10 dollar bills contribute 10*(x+4) to the total.
$10 dollar bills contribute 20*x to the total.
The equation for the total is
5*(2x) + 10*(x+4) + 20x = 400, or
10x + 10x + 40 + 20x = 400, or
40x = 400-40 = 360,
x = 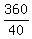 = 9.
Answer. There were 9 $20-dollar bills, 9+4 = 13 $10-dollar bills, and 18 $5-dollar bills.
|
|
|
