Question 1056011: The coordinates of the vertices of quadrilateral NOVA are (-1,4), (4,7), (7,2) and (2,-1) respectively. Classify quadrilateral NOVA (square, rectangle or rhombus)
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! The wording suggests that square, rectangle or rhombus are the only choices,
as if they are telling you that it is not any quadrilateral,
but one of those 3 kinds of parallelograms.
Was that what was really meant?
If you never learned about slopes,
that must be what was meant.
Calculating  you could verify you could verify
if a quadrilateral is a rectangle, a square or a rhombus.
In a square or a rhombus, all 4 sides have the same length.
In a square of a rectangle, both diagonals have the same length.
The  of the segments (sides or diagonals) would tell you if they are parallel or perpendicular, or neither, of the segments (sides or diagonals) would tell you if they are parallel or perpendicular, or neither,
and that would allow you to know if a quadrilateral is a parallelogram,
and in that case it would tell you what kind.
In a parallelogram, opposite sides are parallel;
in a rectangle, adjacent sides are perpendicular to each other,
and in a rhombus,the diagonals are prependicular to each other.
CALCULATING LENGTHS ONLY:
The "formula" for calculating the length of a line segment,
is often called "the distance formula" ,
because it is the distance between the end points of the segment.
It is not really a formula to be memorized,
because it is just the application of the Pythagorean theorem
to the right triangles formed when you draw the segment between the points,
and through each point draw lines parallel to the x- and y-axes.
For segment 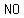 , the length could be calculated by the formula , the length could be calculated by the formula
 , ,
but since  , ,  , ,
and that means that you do not need to worry about which way you write the squared differences.
So, the lengths of the sides are
 , ,
 , ,
 , and , and  . .
The lengths of the diagonals are
 , and , and
 . .
Since all four sides have the same  length, length,
and both diagonals have the same 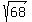 length, length,
quadrilateral  is a square. is a square.
I would also call it a rectangle and a rhombus,
because a square is a special kind of rectangle (one with all sides having the same length),
and a special kind of rhombus (one with all angles having the same measure).
CALCULATING SLOPES:
A short way to write the definition for slope is  , ,
but that assumes you know that  means slope, and that means slope, and that  means change (increase really). means change (increase really).
So, they usually make you write something more complicated, like
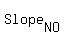   . .
There, the increase in  as you go from as you go from  to to  is is  , and , and
the increase in  as you go from as you go from  to to  is is 
That "formula" is a definition of the word slope.
You just need to remember its meaning,
because that is not something you can deduce by reasoning,
but it is not really a complicated "formula" that you need to memorize.
So, we use that type of "formula" to calculate the slopes of sides 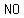 , , 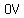 , , 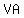 , and , and 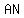 . .
When I fill numbers into that formula,
I first fill the x and y of one point,
and then I fill the coordinates of the other point,
to avoid mistakes.
I would first enter the coordinates for  to get to get  , ,
and then I would fill the blanks with the coordinates for  , to get , to get
 , which is what my teacher would see. Then, , which is what my teacher would see. Then,
 , and , and
 . .
The other sides' slopes can be calculated the same way:


 . .
Since  , sides , sides 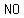 and and 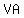 are parallel. are parallel.
Since  , sides , sides 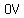 and and 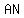 are parallel. are parallel.
So, quadrilateral NOVA is a parallelogram.
Since  , sides , sides 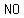 and and 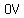 are perpendicular, are perpendicular,
and a parallelogram with one right angle has four right angles,
so quadrilateral NOVA is at least a rectangle.
More specifically, it could also be a square,
which is a special kind of rectangle,
and (according to many definitions) a special kind of rhombus.
to find out if it is a square (and a rhombus),
we can check to see if all sides have the same length,
or we can calculate the slopes of diagonals to see if they are perpendicular.
|
|
|