Question 1055926: I'm having trouble with this mixture problem. The back of the book says the answer is 590 but I think this is wrong, anyway I'm stumped. Any help with this would be much appreciated. Here it is.
Northern Maywood voted 60%to 40% in favor of a water project. Southern Maywood voted 90% to 10% against the project. The project passed 55% to 45%. If 5900 people voted, how many were from Southern Maywood.
Found 2 solutions by josmiceli, MathTherapy:
Answer by josmiceli(19441)   (Show Source): (Show Source):
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website! I'm having trouble with this mixture problem. The back of the book says the answer is 590 but I think this is wrong, anyway I'm stumped. Any help with this would be much appreciated. Here it is.
Northern Maywood voted 60%to 40% in favor of a water project. Southern Maywood voted 90% to 10% against the project. The project passed 55% to 45%. If 5900 people voted, how many were from Southern Maywood.
Let number of voters from Southern Maywood be S
Then number of voters from Northern Maywood = 5,900 – S
Number of voters in Northern Maywood, who voted FOR the project: 60% of (5,900 – S), or .6(5,900 – S)
Number of voters in Southern Maywood who voted FOR the project: 10% of S, or .1S
Since 55% voted FOR the project, we get: .6(5,900 – S) + .1S = .55(5,900)
3,540 - .6S + .1S = 3,245
- .6S + .1S = 3,245 – 3,540
- .5S = - 295
S, or number of voters from Southern Maywood = 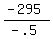 , or , or 
|
|
|