Question 1055828: Given that four integers are consecutive terms of an arithmetic sequence with sum 24 and product 945, what is the biggest of these four integers?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! Since it is about 4 integers, consider divisibility.
 is the factorization for 945. is the factorization for 945.
You notice that 3, 5, and 7 are factors of 945,
and the form an arithmetic sequence!
If those were 3 of the 4 factors whose product is 954,
The fourth factor would be
 . .
So,  , ,
and those 4 factors form an arithmetic sequence.
Of course,  , ,  , ,  , and , and  are another answer. are another answer.
USING EQUATIONS:
 = common difference of the arithmetic sequence. = common difference of the arithmetic sequence.
 = average (mean) and median of thev4 numbers. = average (mean) and median of thev4 numbers.
Then, the numbers are
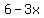 , ,  , , 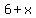 , and , and 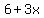 . .
The product is








So,
EITHER, ---> --->  , ,
which gives you the two arithmetic sequences found before,
OR  , which gives you , which gives you
two arithmetic sequences of four (irrational) numbers,
asking up to 24, and with a product of 945.
|
|
|