Question 105571: Find the slope of the line passing through the points (-9,3) and (4,-2)
Answer by bucky(2189)   (Show Source):
You can put this solution on YOUR website! Given the points (-9,3) and (4,-2)
.
To find the slope M of the line joining these two points you can use the formula:
.
.
If you let the point {-9, 3) be the first point ... meaning its values of x and y are
 and  ... then the second point is (4, -2) which means that
its x and y values are  and  respectively. Then just plug these
values into their locations in the formula and you get:
.
.
So the slope is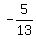 
.
You might be able to speed up the process and to do it in your head by just looking at
the points (-9, 3) and (4, -2) and say to yourself:
.
To go from the x value of the first point to the x value of the second point, I would go
from -9 to +4. This means that on the x-axis I would move from the left to the right 13
numbers or +13. At the same time, to go from the y value of the first point to the y-value
of the second point I would go from +3 to -2 in the y-direction. Since I am moving down
the change is negative, and the number of units to get from +3 to -2 is 5, so the change is
-5 units. This means the slope is -5 divided by +13 which again gives the answer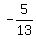
.
Hope this helps you to understand the problem a little better.
|
|
|
