Question 1055624: The average of 3 consecutive odd numbers is 39. What is the sum of the first 2 numbers?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! QUICK MENTAL MATH (good for tests like the SAT):
The average for 3 (or 5, or 7, or ...) equally spaced numbers is
the number in the middle.
So, the 3 consecutive odd numbers are 37, 39, and 41.
The sum of the first 2 of those numbers is 37+39=76 .
SHOWING YOUR WORK:
If you have to justify why the average (also called the mean)
of 3 (or 5, or 7, or ...) equally spaced numbers is
the number in the middle of the ordered list
(also called the median),
the written down explanation below works better.
 = the first of the 3 consecutive odd numbers = the first of the 3 consecutive odd numbers
 = the second one of the 3 consecutive odd numbers = the second one of the 3 consecutive odd numbers
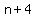 = the third one of the 3 consecutive odd numbers = the third one of the 3 consecutive odd numbers
 is the average of the 3 consecutive odd numbers. is the average of the 3 consecutive odd numbers.
Solving that equation, we get









So, the second of 3 consecutive odd numbers is  , ,
and the sum of the first 2 numbers is

|
|
|