Question 1055589: In a collection of nickels, dimes and quarters, there are twice as many dimes as nickels and 3 fewer quarters than dimes. If the total value of the coins is 4.50 how many of each type of coin are there
Answer by ikleyn(52878)   (Show Source):
You can put this solution on YOUR website! .
In a collection of nickels, dimes and quarters, there are twice as many dimes as nickels and 3 fewer quarters than dimes.
If the total value of the coins is 4.50 how many of each type of coin are there
~~~~~~~~~~~~~~~~~~~~~~~~~~~~
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
* Santa Claus came to us to help solving this problem *
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
He brought 3 quarters and added it to the collection.
The "value" of the collection became $4.50 + 3*$0.25 = $5.25 = 525 cents.
Now we can combine all the coins in groups in a way that each group contains 2 dimes, 1 nickel and 2 quarters.
Each group worth is 2*10 + 5 + 2*25 = 75 cents.
How many groups are there?
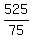 = 7.
OK. Then 7 groups contain 2*7 = 14 dimes, 7 nickels and 2*7 = 14 quarters.
Now we need to return 3 quarters to Santa.
Thank you, Santa !!
Answer. The collection has 14 dimes, 7 nickels and 14-3 = 11 quarters.
In this calculation we can not make a mistake.
Therefore, please check it on your own if the solution is correct.
***************************
Thank you Santa again !!
***************************
In his bag, Santa brought to you the entire bunch of lessons on coin problems
- Coin problems
- More Coin problems
- Solving coin problems without using equations
- Kevin and Randy Muise have a jar containing coins
- Typical coin problems from the archive
- More complicated coin problems
Read them and become an expert in solution of coin problems.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this online textbook under the topic "Coin problems".
|
|
|
