SOLUTION: Three friends anil, bala and chetan, from X to town X to town Y which was 4o km. Anil who had a bike started along with bala while chetan started simultaneously on foot. After some

Below is the sketch to solve the problem:

                       d     d
     X--------------p-----c-----q--------------Y


You see the points X and Y here. The distance between X and Y is 40 kilometers.
The point q is the point where Anil dropped Bala on the way and went back to pick up Chetan.
The point p is the point where Anil picked up Chetan.

So, the Anil's   way is  Xq, then qp,  then pY.
    the Bala's   way is  Xq  biking    with Anil, then qY walking.
    the Chetan's way is  Xp  walking,  then  pY   biking with Anil.

The point "c" is the central point at the half of the distance between X and Y.

From the symmetry, it is clear that the distance Xp is equal to qY.
     The ratio for it is the fact from the condition that all three travelers came to Y simultaneously.
It means that pc = qc, and all we need to do is to find the length pc or qc.
I marked this distance as "d" in the sketch:  d = pc = qc.

Anil on his bike covered the distance of  Xq + 2d + 2d + qY = 40 + 4d.
He spent  hours for the entire journey.

Bala   spent  hours.

Chetan spent 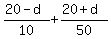 hours, the same time as Bala.

So, the equation to find the unknown "d" is

 = .

Actually, the problem is just setup and, therefore, solved.
The rest is just arithmetic.

The answer is d = 10 km.

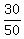So, Xq =  = 30 kilometers, and Anil covered Xq in  =  of an hour = 3*12 = 36 minutes.
It is the time after which Anil turned back.