.
a large rock is thrown upward at a velocity of 16 feet per second from the height of 96 feet above the ground.
how many seconds after it is release does the rock reach its highest point?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Answer. t =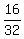 
= 0.5 second.
Solution 1 (Physics)
It is a uniformly decelerated movement with the initial velocity 16 ft/s and deceleration of 32 ft/s^2 (free fall acceleration).
Hence, vertical velocity as a function of time is u(t) = 16 - 32*t.
The maximum height is reached when u(t) = 0, or 16 - 32t = 0, or t = 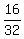= 0.5 s.
Solution 2 (Math, Algebra-I)
The height as the function of time is
h(t) =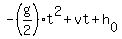 
= 
, (*)
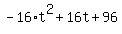where g = 32 ft/s^2 is the free fall acceleration, 16 = 16 ft/s is the initial velocity and 
is the initial height.
The quadratic function (*) has the maximum at
t = 
= 
.
The same answer: t = 0.5 seconds.
See the lessons
- Problem on an arrow shot vertically upward
- Problem on a ball thrown vertically up from the top of a tower
and the lessons
- HOW TO complete the square to find the minimum/maximum of a quadratic function
- Briefly on finding the minimum/maximum of a quadratic function
- HOW TO complete the square to find the vertex of a parabola
- Briefly on finding the vertex of a parabola
in this site.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this online textbook.
The first two lessons are under the topic "Projectiles launched/thrown and moving vertically up and down".
The last four lessons are under the topic "Finding minimum/maximum of quadratic functions".
