.
Find the length of the shorter leg of a right triangle if the longer leg is 8 feet more than the shorter leg
and the hypotenuse is 8 feet less than twice the shorter leg
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Let x = the length (in ft) of the shorter leg of a right triangle.
Then the longer leg is (x+8) feet.
The hypotenuse is 2x-8.
The Pythagorean theorem says
x^2 + (x+8)^2 = (2x-8)^2.
Simplify and solve for x:
= 
,
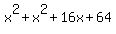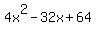2x^2 - 48x = 0,
x^2 - 24x = 0,
x(x-24) = 0.
The shorter leg is 24 ft. The longer leg is 32 ft. The hypotenuse is 2*24-8 = 40 ft.
And the check is 24^2 + 32^2 = 40^2.
It is (3,4,5)-right-angled triangle.
