Question 1055333: If Sarah was saving for a computer that cost$1200 the first month she saved$20 and doubled the amount each month after that how many months will it take her to save the money?
Found 3 solutions by Boreal, stanbon, MathTherapy:
Answer by Boreal(15235)   (Show Source): (Show Source):
You can put this solution on YOUR website! Two ways to do this.
First is brute force
$20+$40+$80+$160+$320+$640=$1260. She will make it in the 5th month.
---------------------
Algebraically
sum of 20*2^(n-1)>=$1200, for n=1 to some number k
factor out a 20 and divide both sides by 20
sum of 2^(n-1), for n=1 to k=60
It is a geometric series where a1=2 and the ratio is 2.
Sum is a1{{1-r^k)/(1-r)}=2(1-r^k)/-1 is greater than = 60
2(1-r^k) is less than or equal to -60
(1-2^k) is <=-30
-2^k <=-31
2^k>=31; k=5
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! If Sarah was saving for a computer that cost $1200 the first month she saved$20 and doubled the amount each month after that how many months will it take her to save the money?
-------
1st mth:: 20
2nd mth:: 40
3rd mth:: 40
etc
----
20 + 40x = 1200
40x = 1180
x = 29.5
Ans:: 30 mths when rounded up
-----------
Cheers,
Stan H.
-----------
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website! If Sarah was saving for a computer that cost$1200 the first month she saved$20 and doubled the amount each month after that how many months will it take her to save the money?
Month 1: $20 saved
Month 2: 2(20), or $40 saved
Month 3: 2(40), or $80 saved
The above represents a GP with the following sequence:  , with:
n = number (month) of the sequence
We now use the sum of a GP, or , with:
n = number (month) of the sequence
We now use the sum of a GP, or 
 ------- Substituting ------- Substituting 

 -------- Cross-multiplying -------- Cross-multiplying


 , or $610
As seen above, the term, or month that she will have saved 1,200 or more is the one in which she has saved $610, or more
Now we see that: , or $610
As seen above, the term, or month that she will have saved 1,200 or more is the one in which she has saved $610, or more
Now we see that:  becomes: becomes:

 ------ Dividing by 20 ------ Dividing by 20

 ------- Converting to LOGARITHMIC form
n, or month in which she will have saved $610 = ------- Converting to LOGARITHMIC form
n, or month in which she will have saved $610 = 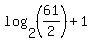 , or , or  .
This means that in month 5, she would NOT HAVE realized her goal of $1,200, but in month 6, she would’ve saved more than the $1,200 (see table below).
OR
The EASIEST METHOD:
Month Amount Saved Total Saved
1 $20 $20
2 2(20) = $40 $60
3 2(40) = $80 $140
4 2(80) = $160 $300
5 2(160) = $320 $620
6 2(320) = $640 $1,260 .
This means that in month 5, she would NOT HAVE realized her goal of $1,200, but in month 6, she would’ve saved more than the $1,200 (see table below).
OR
The EASIEST METHOD:
Month Amount Saved Total Saved
1 $20 $20
2 2(20) = $40 $60
3 2(40) = $80 $140
4 2(80) = $160 $300
5 2(160) = $320 $620
6 2(320) = $640 $1,260
|
|
|