SOLUTION: a function value and a qudrant are given, find the other five function values. give exact answers. cotθ = -3, quadrant IV sinθ = cosθ = tanθ = csc

We draw an angle in the 4th quadrant like below.  Since the cotangent is the
adjacent over the opposite, or , we make the given cotangent,-3, into a
fraction 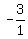, but in quadrant IV, x goes right and y goes down, so the
numerator x is positive and the denominator y is negative, so we change the 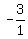 to 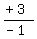 and make the numerator
+3 be the value of x and the denominator -1 be the value of y.

so we have:    
 
 


Now we need to know that 

the sine is the opposite over the hypotenuse or y/r, which is 
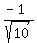 or . 

the cosine is the adjacent over the hypotenuse or x/r, which is 
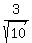 or .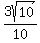 

the tangent is the opposite over the adjacent or y/x, which is 
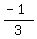 or . 

the secant is the hypotenuse over the adjacent or r/x, which is 
. 

the cosecant is the hypotenuse over the opposite or r/y, which is 
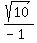 or . 

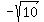Edwin