Question 1055178: What is the minimum distance between the 2 parabolas:
y = x^2+4 and x = y^2 ?
Answer by Fombitz(32388)   (Show Source): (Show Source):
You can put this solution on YOUR website! OK, assume that the shortest distance line segment intersects the first curve at ( , ,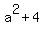 ) and intersects the second curve at ( ) and intersects the second curve at ( , , ). ).
The slope of the tangent line of the first curve at point  would be would be  since since  . .
The slope of the tangent line of the second curve at point  would be would be 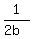 since since  . .
The slopes are equivalent which leads to the first equation,


.
.
.
Now use the distance formula (actually use the distance squared to eliminate the square root) with the two points of intersection,

From the previous equation,

Substitute,

Graphing and finding the minimum,

So then,


.
.
.
 . .
.
.
.
So then the points are (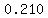 , ,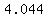 ) and ( ) and (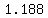 , , ) )
Using the distance formula,

You could also have just used the graphed value when we minimized the distance squared,


.
.
.
 . .
|
|
|