Question 1055142: x^2 - 6x- (x^2 -6x - 3 )^1/2 =5
Found 2 solutions by Edwin McCravy, ikleyn:
Answer by Edwin McCravy(20055)   (Show Source): (Show Source):
You can put this solution on YOUR website!
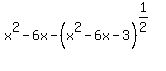   Since x²-6x appears twice, let u = x²-6x
Since x²-6x appears twice, let u = x²-6x
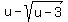   Isolate the square root on the right side:
Isolate the square root on the right side:
  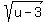 Square both sides
Square both sides
  
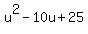  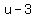 Get 0 on the right
Get 0 on the right
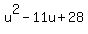   Factor the left side:
(u-4)(u-7) = 0
u-4 = 0; u = 7
u = 4; u = 7
Since u = x²-6x
x²-6x = 4; x²-6x = 7
x²-6x-4 = 0; x²-6x-7 = 0
(x-7)(x+1) = 0
x-7 = 0; x+1 = 0
x = 7; x = -1
Since x²-6x-4 does not factor
Factor the left side:
(u-4)(u-7) = 0
u-4 = 0; u = 7
u = 4; u = 7
Since u = x²-6x
x²-6x = 4; x²-6x = 7
x²-6x-4 = 0; x²-6x-7 = 0
(x-7)(x+1) = 0
x-7 = 0; x+1 = 0
x = 7; x = -1
Since x²-6x-4 does not factor
  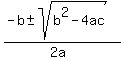
  
  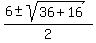
  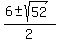
  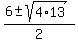
  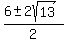
  
  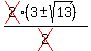
  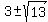 Four potential solutions.
7, -1,
Four potential solutions.
7, -1, 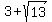 , , 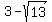 But we must check all solutions when there is a square
root radical with a variable underneath contained in the
original equation.
Checking x=7 in the original equation:
But we must check all solutions when there is a square
root radical with a variable underneath contained in the
original equation.
Checking x=7 in the original equation:
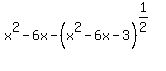  
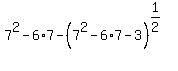  



  
   That checks, So x=7 IS a solution
Checking x=-1 in the original equation:
That checks, So x=7 IS a solution
Checking x=-1 in the original equation:
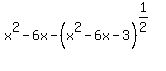  
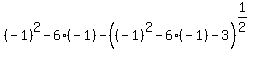  



  
   That checks, So x=-1 IS a solution
Checking x=3 + sqrt(13) in the original equation:
That checks, So x=-1 IS a solution
Checking x=3 + sqrt(13) in the original equation:
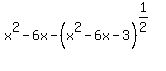   That's too hard to substitute in so, do it on
your TI-84:
Type in
That's too hard to substitute in so, do it on
your TI-84:
Type in 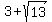 Press STO
Press ALPHA STO ENTER
Type in
Press STO
Press ALPHA STO ENTER
Type in 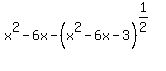 Press ENTER
Read 3.
Since 3 is not 5, 3 + sqrt(13) is an EXTRANEOUS answer,
so we discard it.
Checking x=3 - sqrt(13) in the original equation:
Press ENTER
Read 3.
Since 3 is not 5, 3 + sqrt(13) is an EXTRANEOUS answer,
so we discard it.
Checking x=3 - sqrt(13) in the original equation:
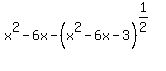   That's also too hard to substitute in so, do it on
your TI-84:
Type in
That's also too hard to substitute in so, do it on
your TI-84:
Type in 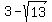 Press STO
Press ALPHA STO ENTER
Type in
Press STO
Press ALPHA STO ENTER
Type in 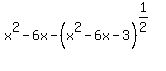 Press ENTER
Read 3.
Since 3 is not 5, 3 - sqrt(13) is also an EXTRANEOUS answer,
so we discard it.
The only solutions are 7 and -1.
Edwin
Press ENTER
Read 3.
Since 3 is not 5, 3 - sqrt(13) is also an EXTRANEOUS answer,
so we discard it.
The only solutions are 7 and -1.
Edwin
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
x^2 - 6x- (x^2 -6x - 3 )^1/2 =5
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Below find more short solution.
x^2 - 6x- (x^2 -6x - 3 )^1/2 =5 --->
(x^2 - 6x -3) - (x^2 -6x - 3 )^1/2 = 2. (*)
Introduce new variable
u = (x^2 -6x - 3 )^1/2.
Then the equation (*) takes the form
u^2 - u = 2, or
u^2 - u - 2 = 0.
Factor:
(u-2)*(u+1) = 0.
The roots are u = 2 and u = -1.
Now you have this equations for x:
(x^2 -6x - 3 )^1/2 = 2 ---> x^2 -6x - 3 = 4 ---> x^2 -6x -7 = 0.
Factor: (x-7)*(x+1) = 0 ---> the roots are x= 7 and x= -1.
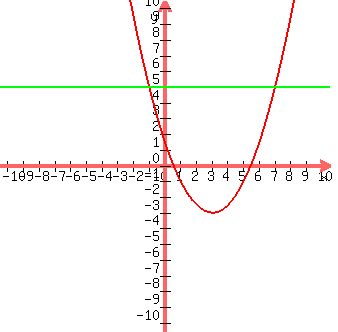
Plot y = 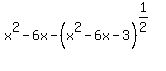 and y = 5 and y = 5
|
|
|