Question 1055058: Determine the equation of the parabola that has its vertex at the origin and satisfies the given conditions?
Axis is the x-axis and p=2
Axis is the x-axis and the parabola passes through the point (4,2)
Write the equation in standard form.Determine the vertex ,axis and the direction in which each parabola opens
X^2-x+3y+1=0
X^2+2x+2y+3=0
Answer by josgarithmetic(39617)   (Show Source):
You can put this solution on YOUR website! The first two example parts of the question take an equation form,  , which you would be able to derive if you assumed a given vertex, directrix, focus. See a video about the derivation or the discussion in your textbook.
The example for p=2 would give  , and since you're also given that vertex is the origin, (0,0), the equation becomes simply  . If you want this in the more typical standard form, then x= .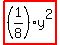
The example for the parabola to contain point (4,2), and axis of symmetry still be x axis, means you have or better,  ; and you use the given included point to find the value of p.
-
and putting in the coordinates for the point,
-
and this finished equation is  .
|
|
|
