|
Question 1054848:
You want to purchase a new car in 9
years and expect the car to cost $81 comma 000
.
Your bank offers a plan with a guaranteed APR of 6.5 %
if you make regular monthly deposits. How much should you deposit each month to end up with $81 comma 000
in 9
years?
Found 2 solutions by Boreal, Theo:
Answer by Boreal(15235)   (Show Source): (Show Source):
You can put this solution on YOUR website! The general formula is A (at end)=d (deposit)(1+(r/n)^nt-1)/(r/n); where r is the rate, n the number of compoundings per year and nt is the total number of compoundings.
A=d [{1+(.065)/12))^108-1)]/(.065/12)
A=d[(1.792)-1]/(.065/12)=81,000, but don't round yet
multiply through by (0.065/12) without rounding
438.75=d(1.792-1);
d=$553.87
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! translation:
You want to purchase a new car in 9 years and expect the car to cost 81,000.
Your bank offers a plan with a guaranteed APR of 6.5 %
If you make regular monthly deposits, how much should you deposit each month to end up with 81,000 in 9 years?
the easiest way to do this is to use a financial calculator.
one such calculator can be found here:
http://arachnoid.com/finance/index.html
my inputs and output are shown below:
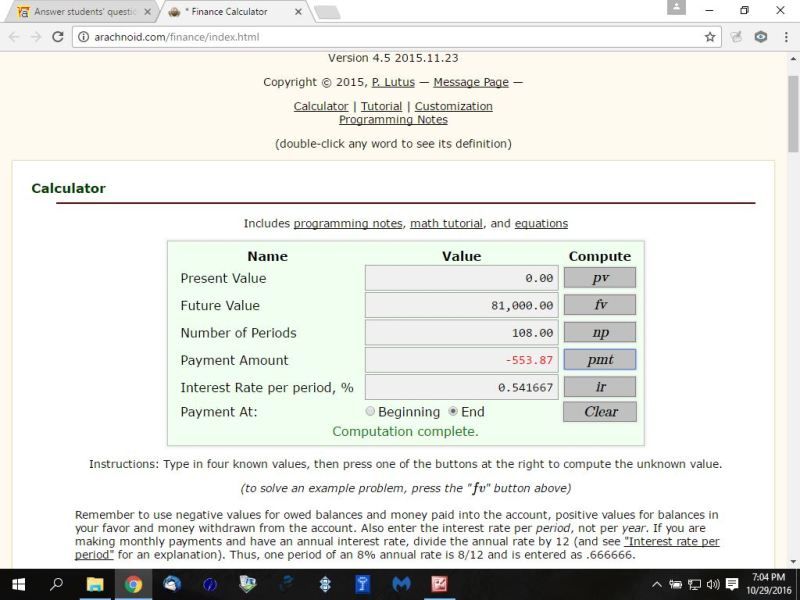
i entered present value as 0
i entered future value as 81000
i entered number of periods as 108
i entered interest reater per period % as 6.5 / 12 = .541667
i entered payment at end of period
i then clicked on pmt and it then told me that the payment amount was 553.87.
i disregarded the sign as irrelevant to what i was trying to do.
it has to do with money coming in and money going out.
if future value was money coming in, then payment amount was money going out.
the payment amount was money going out from me to the bank, therefore the sign of the result was negative.
that's because i showed the future value as positive which meant it was money coming in to me at the end of the 108 months.
you would deposit 553.87 at the end of each month at 6.5% per year compounded monthly and you would have 81,000 at the end of the 108 months.
|
|
|
| |