.
Use a Double- or Half-Angle Formula to solve the equation in the interval [0, 2π). (Enter your answers as a comma-separated list.)
cos(2θ) + sin2(θ) = 0
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
What is 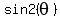 ? Is it
? Is it  ?
You use so complicated terminology and are not able to write the equation in an unambiguous way?
I see a disproportion in it.
?
You use so complicated terminology and are not able to write the equation in an unambiguous way?
I see a disproportion in it.
OK, I will assume that the equation is
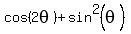 = 0.
Use the double-angle formula
= 0.
Use the double-angle formula 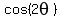 =
= 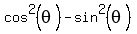 and replace
and replace 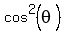 by
by 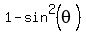 .
Then you will get
.
Then you will get 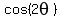 =
= 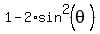 .
Thus the original equation takes the form
.
Thus the original equation takes the form
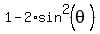 +
+  = 0, or
= 0, or
 = 1, or
= 1, or
 = +/-1.
Answer.
= +/-1.
Answer.  =
=  , k = 0, +/-1, +/-2, . . .
, k = 0, +/-1, +/-2, . . .