You didn't put enough parentheses when you typed in your equation:
It should be:
1/(x+4)=2/(x^2+3x-4)-1/(1-x)
not this 1/x+4=2/x^2+3x-4-1/1-x
You want it to mean the same as this:
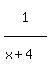
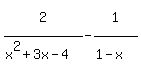Not the same as this 
--------------------------------------------------
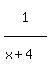
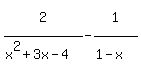Before we get a common denominator we must simplify.
We factor the denominator x²+3x-4 as (x+4)(x-1) and change
the denominator 1-x to descending order -x+1, and then
factor out a negative sign as -(x-1) by changing the
sign inside the parentheses. So now we have
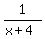
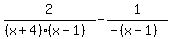or
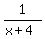
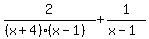<--eq. #1
Now the common denominator is (x+4)(x-1). Since it is
an equation and not just an expression without an equal
sign, we may multiply both sides by the LCD over 1, which
I'll write as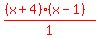 
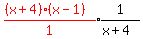
Notice that we have multiplied that LCD by every term of
eq. #1 above.
Now we can cancel and eventually we'll end up with no fractions:
And if we ignore the ones in the denominators, we have just:
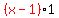
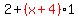or
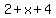
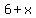Subtract x from both sides:
This is false, so there is no solution
to the given problem, but we could not
have known that it had no solution until
we got to a false equation containing no
variables. Other very similar equations
to this one do have solutions because the
variables x's don't all cancel out as they
did in this equation.
Edwin
