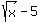SOLUTION: {{{"f(x)"}}}{{{""=""}}}{{{sqrt(x)-5}}} A. f -1 (x) = x 2 + 25; y ≥ 25 B. f -1 (x) = x 2 + 5; y ≥ 5 C. f -1 (x) = (x + 5) 2; y ≥ 5 D. f

Algebra ->  Real-numbers -> SOLUTION: {{{"f(x)"}}}{{{""=""}}}{{{sqrt(x)-5}}} A. f -1 (x) = x 2 + 25; y ≥ 25 B. f -1 (x) = x 2 + 5; y ≥ 5 C. f -1 (x) = (x + 5) 2; y ≥ 5 D. f       Log On


   

Question 1054387: %22f%28x%29%22%22%22=%22%22sqrt%28x%29-5
A.
f -1 (x) = x 2 + 25; y ≥ 25
B.
f -1 (x) = x 2 + 5; y ≥ 5
C.
f -1 (x) = (x + 5) 2; y ≥ 5
D.
f -1 (x) = x 2 + 25; y > 5
Answer by Edwin McCravy(20055) About Me  (Show Source):
You can put this solution on YOUR website!
%22f%28x%29%22%22%22=%22%22sqrt%28x%29-5

Draw the graph and also the graph of the identity line
which has equation y = x.  The green dotted line is the 
identity line.  The graph of the inverse function f-1 
is the reflection of the red graph across the identity line.



Then substitute y for f(x)

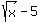y%22%22=%22%22sqrt%28x%29-5

Interchange x and y:

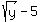x%22%22=%22%22sqrt%28y%29-5

Solve for y:

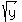
x%2B5%22%22=%22%22sqrt%28y%29

%28x%2B5%29%5E2%22%22=%22%22y

y%22%22=%22%22%28x%2B5%29%5E2

Draw the graph on the same axes to see if we 
need to restrict it, and if so how:


 
So we see that we only want to keep the part of that
graph to the right of x = -5, so it will be the reflection
of the first graph in the green identity line.

So to do that we must restrict the graph on the left 
to value of x greater than or equal to -5, so the graph
on the left will look like this, and contain only the
reflection of the first graph as we see below:



So we take the equation

y%22%22=%22%22%28x%2B5%29%5E2

Replace y by f-1(x)

And put the restriction x ≥ -5 after it:

Answer: f-1(x) = (x+5)2; x ≥ -5

You don't have that listed with the correct restriction,

Also restrictions are usually always give with x rather than 
y.  All the choices you have listed above have only y, not x.
Did you copy the problem wrong?

Edwin