SOLUTION: How many positive integers n make the expression 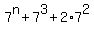{{{7^n +7^3 + 2 * 7^2}}} a perfect square?

Calculate 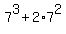 = 441 and notice that 441 = .

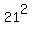Now your equation is

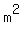 =  for some integer "m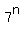",  or

 = ,  or

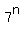 = (m+21)*(m-21).

Since "7" is a prime number, both (m+21) and (m-21) must be degrees of 7.

So, ask yourself: what are two degrees of 7 that differs by 42 = (m+21)-(m-21).

The answer is OBVIOUS: these degrees are 7 and , and there are NO others.

So, there is only ONE possible value of "n": n = 3.

The other value n=16 of the other tutor is a MISTAKE.