|
Question 1053721: 4x^2 + 9y^2 = 72
x - y^2 = -1
Select all of the following that are solutions to the system shown.
Found 2 solutions by Fombitz, ikleyn:
Answer by Fombitz(32388)   (Show Source): (Show Source):
Answer by ikleyn(52786)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
4x^2 + 9y^2 = 72
x - y^2 = -1
Select all of the following that are solutions to the system shown.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
4x^2 + 9y^2 = 72, (1)
x - y^2 = -1. (2)
To solve it algebraically, express y^2 = x+1 from the equation (2) and substitute it into equation (1). You will get
4x^2 + 9(x+1) = 72.
In this way you got a single equation for only one unknown x.
Simplify and solve it:
4x^2 + 9x - 63 = 0,
 = = 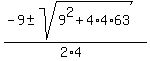 = =  . .
 = =  = 3, = 3,  = = 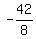 = -5.25.
The negative root doesn't suit the equation y^2 = x+1, since the right site would be negative.
So, the only solution for x is x=3.
Then you get two solutions for y: y^2 = x+1 = 3+1 = 4 and = -5.25.
The negative root doesn't suit the equation y^2 = x+1, since the right site would be negative.
So, the only solution for x is x=3.
Then you get two solutions for y: y^2 = x+1 = 3+1 = 4 and  = 2, = 2,  = -2.
Answer. The system has two solutions (x,y) = (3,2) and (x,y) = (3,-2). = -2.
Answer. The system has two solutions (x,y) = (3,2) and (x,y) = (3,-2).
For many other solved similar problems see the lessons
- Solving systems of algebraic equations of degree 2 and degree 1
- Solving systems of algebraic equations of degree 2
in this site.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this online textbook under the topic "Systems of equations that are not linear".
|
|
|
| |