Question 1053297: The average of four consecutive positive odd integers is less than 20. What are the greatest integers that will satisfy the condition?
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! Let  ,  ,  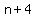,  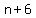be the four consecutive odd integers.
The average of those four numbers is
 .
We need to find the greatest odd integer that will satisfy
 <---> <---> .
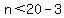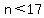The answer is obviously  ,
so  ,  ,  , and  are four consecutive positive odd integers whose average is less than 20,
and there are no set of greater consecutive odd positive integers with an average that is less than 20.
If you are answering that as a question for the SAT, quickly and without writing equations,
you should know that for a set of equally spaced numbers (an arithmetic sequence),
the average is the median.
The median of 3 (or 5, or 7, etc) such numbers is the middle number.
The median of 4 (or 6, or 8, etc) such numbers is the number midway between the two middle ones.
The median of 4 consecutive positive odd integers is the even integer between the two middle consecutive positive odd integers.
the greatest even number less than 20 is  ,
so the two middle consecutive positive odd integers are
 and  ,
so the other two of the four consecutive positive odd integers must be
 and  .
An SAT star can think through that faster than I can type the answers.
|
|
|
