Question 1053273: Find an exponential equation,f(x),for a curve that passes through (-1,-1/3) and (3,-27/16).
Answer by htmentor(1343)   (Show Source):
You can put this solution on YOUR website! An exponential function has the form y = f(x) = a*b^x
We have two unknowns, the coefficients a and b.
But we can form two equations from the two (x,y) pairs and solve.
The curve passes through (-1,-1/3), so we can write -1/3 = a*b^(-1) -> -1/3 = a/b, or a = -b/3
So we have y = (-b/3)b^x. Using the other point (3, -27/16) we have
-27/16 = (-b/3)b^3 -> 27/16 = b^4/3
Solve for b: -b^4 = -81/16 -> b = 3/2
Thus a = (-3/2)/3 = -1/2
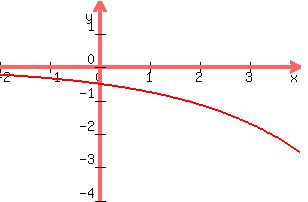
So the equation is f(x) = (-1/2)(3/2)^x
The graph is below:
|
|
|
