SOLUTION: Find the exact value of the​ following, without using a calculator. sin(sin^-1 (1/2)+tan^-1 (-5))

Algebra ->  Trigonometry-basics -> SOLUTION: Find the exact value of the​ following, without using a calculator. sin(sin^-1 (1/2)+tan^-1 (-5))      Log On


   

Question 1052901: Find the exact value of the​ following, without using a calculator.
sin(sin^-1 (1/2)+tan^-1 (-5))
Answer by ikleyn(52792) About Me  (Show Source):
You can put this solution on YOUR website!
.
Find the exact value of the​ following, without using a calculator.
sin(sin^-1 (1/2)+tan^-1 (-5))
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ 

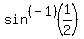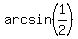0.  Let alpha be sin%5E%28-1%29%281%2F2%29 = arcsin%281%2F2%29, and

    let be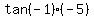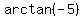ta be tan%28-1%29%28-5%29 = arctan%28-5%29.

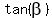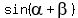    Then we have sin%28alpha%29 = 1%2F2 with alpha in QI and tan%28beta%29 = -5 with beta in QIV, and we need to find sin%28alpha+%2B+beta%29.

    Surely, we will use the formula

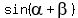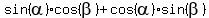    sin%28alpha+%2B+beta%29 = sin%28alpha%29%2Acos%28beta%29+%2B+cos%28alpha%29%2Asin%28beta%29,                 (1)

    but first we shall calculate cos%28beta%29, cos%28alpha%29 and sin%28beta%29.


1.  Since sin%28alpha%29 = 1%2F2, we have alpha = pi%2F6 and cos%28alpha%29 = sqrt%283%29%2F2.    (2)


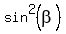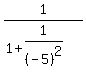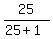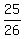2.  sin%5E2%28beta%29 = 1%2F%281%2B1%2Ftan%5E2%28beta%29%29 = 1%2F%281+%2B+1%2F%28-5%29%5E2%29 = 25%2F%2825%2B1%29 = 25%2F26.

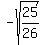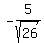    Hence, sin%28beta%29 = -sqrt%2825%2F26%29 = -5%2Fsqrt%2826%29.                            (3)

    We chose the sign "-" at the square root, since the angle beta lies in QIV (due to the sign of tan).


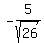3.  Since sin%28beta%29 = -5%2Fsqrt%2826%29, we have 

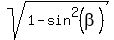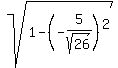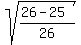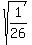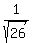    cos%28beta%29 = sqrt%281-sin%5E2%28beta%29%29 = sqrt%281-%28-5%2Fsqrt%2826%29%29%5E2%29 = sqrt%281-25%2F26%29 = sqrt%28%2826-25%29%2F26%29%29 = sqrt%281%2F26%29 = 1%2Fsqrt%2826%29.    (4)


4.  Now you have everything to use the formula (1):

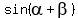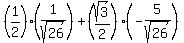    sin%28alpha%2Bbeta%29 = %281%2F2%29%2A%281%2Fsqrt%2826%29%29+%2B+%28sqrt%283%29%2F2%29%2A%28-5%2Fsqrt%2826%29%29 = %281-5%2Asqrt%283%29%29%2F%282%2Asqrt%2826%29%29.

Solved.

For other similar solved problems see the lesson
    - Advanced problems on calculating trigonometric functions of angles
in this site.

Also, you have this free of charge online textbook in ALGEBRA-II in this site
    - ALGEBRA-II - YOUR ONLINE TEXTBOOK.

The referred lesson is the part of this online textbook under the topic "Trigonometry: Solved problems".