Question 1052727: mr. meyers is creating a seating chart for his class. There are 12 desks for 9 students. If he creates a different seating chart for every day, how many days will pass until he has to repeat a seating chart?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! He can assign
Adam to any of the  desks. desks.
In each of those cases, th first choice leaves  choices of seat for Bob. choices of seat for Bob.
For each of the 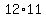 resulting cases, there would be resulting cases, there would be  choices for the seat assigned to Carl. choices for the seat assigned to Carl.
For each of the 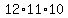 sets of seats assigned to Adam, Bob, and Carl, there would be sets of seats assigned to Adam, Bob, and Carl, there would be  possible places to sit Daniel. possible places to sit Daniel.
So far we have  ways to sit the first 4 students, ways to sit the first 4 students,
and Mr Meyers still has to choose seats for Ed, Frank, George, Harry, and Ian.
All in all, he has  possible seating arrangements. possible seating arrangements.
To go through all 79.8336 million possible seating charts would take him that many days. assuming the class meets for 365 days per year, that would be over 200 thousand years. I do not believe Mr Meyers can live that long.
|
|
|