sinθ= -2/3 and tanθ > 0
-2/3 is a negative number, so the sine is negative.
tanθ > 0 says the tangent is positive.
That tells us that θ is in QIII
So we draw the picture of θ. We know that
 Since
Since  We draw a right triangle in QIII with opposite side -2
and hypotenuse +3. We can use the Pythagorean theorem
to find the adjacent side or x,
adjacent = x =
We draw a right triangle in QIII with opposite side -2
and hypotenuse +3. We can use the Pythagorean theorem
to find the adjacent side or x,
adjacent = x =  We take it negative because x, the adjacent side, goes to
the LEFT of the origin.
We take it negative because x, the adjacent side, goes to
the LEFT of the origin.
 Since
Since  ,
,


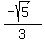

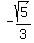 .
Since
.
Since  ,
,
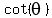

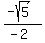

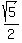 .
Edwin
.
Edwin