|
Question 1051962: The height h(in feet) of the cloud base can be estimated using h=227(T-D) where T is the ground temperature and D is the dew point .. The temperature within a cloud at height h (in feet) above the cloud base T=B-(3/1000)h where B is temperature of cloud at its base using above formulas find a formula for the height h of the freezing level in a cloud of ground temperature G and dew point D
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! The measurement of height in both formulas is clearly specified to be in feet.
unfortunately, the rest is not so clearly defined.
For starters, I assume "the height h of the freezing level" is the height in feet above the ground.
I expected that ground temperature 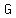 was measured in degrees Celsius, not kelvins, not degrees Fahrenheit, not degrees Rankine. was measured in degrees Celsius, not kelvins, not degrees Fahrenheit, not degrees Rankine.
The same goes for the units of the dew point  , ,
and for the units of temperature and dew point in both formulas.
However, that might be an incorrect assumption, because I found out that the height, in feet, of the cloud base can be estimated using
 or or  when when  =ground temperature is in degrees Fahrenheit. =ground temperature is in degrees Fahrenheit.
It the temperature at the ground is measured in degrees Celsius, then the formula to use would be
 or or  . .
Assuming that temperatures are in degrees Fahrenheit,
 is the height (in feet) of the cloud base. is the height (in feet) of the cloud base.
The other formula says that inside the cloud, at a height of  feet above the ground, feet above the ground,
 . .
One issue is if temperatures for that formula are in degrees Fahrenheit, or in some other unit.
Another problem is how to figure out  , the temperature of cloud at its base. , the temperature of cloud at its base.
Is it the same as 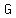 , the ground temperature? , the ground temperature?
I found two references, saying that the air temperature above the ground decreases approximately linearly with height.
One said it decreases by 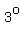  for every 1000 feet. for every 1000 feet.
The other one said 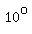  for every kilometer, but that in practice there is usually an extra for every kilometer, but that in practice there is usually an extra 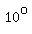  difference near the ground (http://www.weatherjackwx.co.uk/tutorials/tut-various/Bradbury/bradbury.html). difference near the ground (http://www.weatherjackwx.co.uk/tutorials/tut-various/Bradbury/bradbury.html).
Both references were talking about temperature in air below clouds or in cloudless air.
I did not find out what happens inside the lower part of clouds,
where the water is in form of liquid droplets,
but it is probably safe to assume that the same rate of cooling applies as below the clouds.
Then, up to the freezing point, with all temperatures in degrees Celsius,
 , ,
which means that  , and , and
 <---> <--->  . .
So, it seems like the second formula was to be used with temperatures in degrees Celsius,
and that  applies above and below the cloud base, as long as you measure the temperatures in degrees Celsius. applies above and below the cloud base, as long as you measure the temperatures in degrees Celsius.
So, with 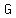 in degrees Celsius, in degrees Celsius,
 } <---> } <--->  } <---> } <---> 
So when  , meaning , meaning   = freezing temperature, = freezing temperature,
 , below of within the cloud. , below of within the cloud.
If you want to know if it is inside the cloud, then you need to see is 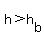 . .
For that you can use
 , with , with 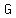 in degrees Celsius, in degrees Celsius,
or  with with 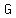 in degrees Fahrenheit. in degrees Fahrenheit.
|
|
|
| |