 The denominator is the only thing not factored,
so factor it
The denominator is the only thing not factored,
so factor it
 The critical numbers are the zeros of all the factors:
0,
The critical numbers are the zeros of all the factors:
0,  , -1, 1, 2
Arrange them in numerical order:
-1, 0, 1,
, -1, 1, 2
Arrange them in numerical order:
-1, 0, 1,  , 2
-1, 0, 1,
, 2
-1, 0, 1, 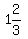 , 2
and put them on a number line:
-----------o----o----o--o-o------
-3 -2 -1 0 1 2 3
Choose test values less than the least, in between
them, and greater than the greatest:
Test values: -2, -0.5, 0.5, 1.5, 1.9, 3
If the test value gives
, 2
and put them on a number line:
-----------o----o----o--o-o------
-3 -2 -1 0 1 2 3
Choose test values less than the least, in between
them, and greater than the greatest:
Test values: -2, -0.5, 0.5, 1.5, 1.9, 3
If the test value gives  when substituted
in the open interval which the test value is in is
part of the solution; otherwise it's not.
Substituting -2 gives 161.333... which is
when substituted
in the open interval which the test value is in is
part of the solution; otherwise it's not.
Substituting -2 gives 161.333... which is  ,
so
,
so 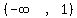 is part of
the solution.
Substituting -0.5 gives 0.176... which is
is part of
the solution.
Substituting -0.5 gives 0.176... which is  ,
so
,
so 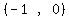 is part of
the solution.
Substituting 0.5 gives 2.296... which is
is part of
the solution.
Substituting 0.5 gives 2.296... which is  ,
so
,
so  is part of
the solution.
Substituting 1.5 gives -31.64... which is
is part of
the solution.
Substituting 1.5 gives -31.64... which is 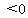 ,
so
,
so 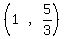 is NOT part of
the solution.
Substituting 1.9 gives -596.71... which is
is NOT part of
the solution.
Substituting 1.9 gives -596.71... which is 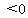 ,
so
,
so 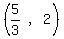 is NOT part of
the solution.
Substituting 3 gives 10368 which is
is NOT part of
the solution.
Substituting 3 gives 10368 which is  ,
so
,
so  is part of
the solution.
The critical numbers from the numerator 0,5/3, and -1
satisfy the given inequality since "equal to 0" is allowed.
However the critical numbers from the denominator, 1 and 2,
do not.
Solution set:
is part of
the solution.
The critical numbers from the numerator 0,5/3, and -1
satisfy the given inequality since "equal to 0" is allowed.
However the critical numbers from the denominator, 1 and 2,
do not.
Solution set:
 Edwin
Edwin